동적 계획법 (Dynamic Programming, DP)

동적 계획법은 컴퓨터 과학과 수학 분야에서 복잡한 문제를 더 간단한 하위 문제로 나누어 해결하는 강력한 알고리즘 설계 기법이다.
이 접근법은 특히 최적화 문제를 해결하는 데 매우 효과적이며, 다양한 응용 분야에서 널리 사용된다.

최적 부분 구조와 중복되는 하위 문제 특성을 가진 문제들에 적용할 수 있으며, 분할 정복과 달리 이미 해결한 하위 문제의 결과를 저장하고 재활용함으로써 계산 효율성을 크게 향상시킨다.

동적 계획법의 기본 개념

동적 계획법(Dynamic Programming, DP)은 복잡한 문제를 여러 개의 겹치는 하위 문제로 나누고, 각 하위 문제를 한 번만 풀어 그 결과를 저장해두고 재활용하는 알고리즘 설계 방법이다.

“동적 계획법"이라는 용어는 1950년대 리처드 벨만(Richard Bellman)이 처음 사용했다. 흥미롭게도, 이 이름은 실제로 수학적 의미보다는 당시 연구 기금을 얻기 위한 전략적 선택이었다고 한다. “프로그래밍"이라는 단어는 여기서 컴퓨터 프로그래밍이 아닌 “계획법” 또는 “의사결정 과정의 최적화"를 의미한다.

핵심 원리

동적 계획법의 두 가지 핵심 원리는 다음과 같다:

  1. 최적 부분 구조(Optimal Substructure): 문제의 최적해가 하위 문제의 최적해로부터 구성될 수 있는 특성이다. 즉, 큰 문제의 최적해를 찾기 위해 더 작은 문제들의 최적해를 활용할 수 있다.
  2. 중복되는 하위 문제(Overlapping Subproblems): 동일한 하위 문제가 알고리즘 실행 과정에서 반복적으로 발생하는 특성이다. 이러한 중복 계산을 피하기 위해 각 하위 문제의 해를 저장하고 재사용한다.

동적 계획법의 접근 방식

동적 계획법은 주로 두 가지 방식으로 구현된다:

  1. 하향식 접근법(Top-down Approach): 큰 문제에서 시작하여 작은 하위 문제로 분할하며, 메모이제이션(memoization)을 통해 이미 해결한 하위 문제의 결과를 저장하고 재사용한다. 주로 재귀적 구현에 사용된다.
  2. 상향식 접근법(Bottom-up Approach): 가장 작은 하위 문제부터 시작하여 점차 큰 문제를 해결해 나가는 방식이다. 테이블링(tabulation) 기법을 사용하여 결과를 테이블에 채워가며 진행한다. 주로 반복적(iterative) 구현에 사용된다.

동적 계획법의 구성 요소

  1. 상태(State) 정의
    동적 계획법에서 “상태"는 문제의 특정 단계나 상황을 나타낸다.
    상태를 명확하게 정의하는 것은 DP 문제 해결의 첫 단계이다.
    상태는 보통 문제의 변수들의 조합으로 표현된다.

    • 피보나치 수열에서 상태는 단순히 현재 계산하려는 수의 인덱스 n이 된다.
    • 배낭 문제에서는 현재 고려 중인 아이템의 인덱스와 남은 용량의 조합이 상태가 된다.

  2. 상태 전이 방정식(State Transition Equation)
    상태 전이 방정식(또는 점화식)은 현재 상태의 해를 이전 상태의 해들로부터 어떻게 계산할 수 있는지 정의한다.
    이 방정식은 문제의 최적 부분 구조를 수학적으로 표현한다.

    • 예를 들어, 피보나치 수열의 상태 전이 방정식은 다음과 같다:
      • F(n) = F(n-1) + F(n-2), n ≥ 2
      • F(0) = 0, F(1) = 1 (기저 조건)

  3. 기저 조건(Base Case)
    기저 조건은 더 이상 작은 하위 문제로 나눌 수 없는 가장 작은 문제의 해를 정의한다.
    이는 재귀적 해결책의 종료 조건이자, 상향식 접근법에서 테이블의 초기값이 된다.

  4. 메모이제이션과 테이블링

    1. 메모이제이션(Memoization): 하향식 접근법에서 사용되는 기법으로, 이미 해결한 하위 문제의 결과를 메모리(보통 배열이나 해시 맵)에 저장하고, 동일한 하위 문제가 다시 발생하면 재계산 없이 저장된 결과를 반환한다.
    2. 테이블링(Tabulation): 상향식 접근법에서 사용되는 기법으로, 작은 하위 문제부터 시작하여 점진적으로 더 큰 문제의 해를 계산하면서 테이블에 결과를 채워간다.

시간 및 공간 복잡도 최적화

메모리 사용 최적화

많은 DP 문제에서 전체 테이블이 아닌 최근의 결과만 필요한 경우가 있다.
이 경우 공간 복잡도를 크게 줄일 수 있다.

1차원 배열로 최적화된 0-1 배낭 문제:

1
2
3
4
5
6
7
8
9

def knapsack_01_optimized(weights, values, capacity):
    n = len(weights)
    dp = [0 for _ in range(capacity + 1)]
    
    for i in range(n):
        for w in range(capacity, weights[i] - 1, -1):  # 역순으로 순회
            dp[w] = max(dp[w], values[i] + dp[w - weights[i]])
    
    return dp[capacity]

이 최적화로 공간 복잡도가 O(n*W)에서 O(W)로 감소한다.

상태 전이 최적화

일부 DP 문제에서는 상태 전이를 최적화하여 시간 복잡도를 줄일 수 있다.

최장 증가 부분 수열(LIS)의 이진 검색 최적화:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def longest_increasing_subsequence_optimized(nums):
    if not nums:
        return 0
    
    # tails[i]는 길이가 i+1인 증가 부분 수열의 마지막 원소 중 가능한 최소값
    tails = []
    
    for num in nums:
        # 이진 검색으로 num이 들어갈 위치 찾기
        left, right = 0, len(tails)
        while left < right:
            mid = (left + right) // 2
            if tails[mid] < num:
                left = mid + 1
            else:
                right = mid
        
        # num을 적절한 위치에 삽입하거나 업데이트
        if left == len(tails):
            tails.append(num)
        else:
            tails[left] = num
    
    return len(tails)

슬라이딩 윈도우 최적화

일부 DP 문제에서는 각 상태를 계산할 때 인접한 몇 개의 이전 상태만 필요한 경우가 있다.
이때 슬라이딩 윈도우 기법을 사용하여 공간 복잡도를 크게 줄일 수 있다.

피보나치 수열의 슬라이딩 윈도우 최적화:

1
2
3
4
5
6
7
8
9

def fibonacci_sliding_window(n):
    if n <= 1:
        return n
    
    a, b = 0, 1
    for _ in range(2, n + 1):
        a, b = b, a + b
    
    return b

이 최적화로 공간 복잡도가 O(n)에서 O(1)로 감소합니다.

분할 정복 최적화

일부 특수한 DP 문제에서는 분할 정복 기법을 적용하여 시간 복잡도를 개선할 수 있다.

Knuth’s Optimization: 이 최적화는 다음 조건을 만족하는 구간 DP 문제에 적용할 수 있다:

  1. 상태 전이 방정식의 형태가 dp[i][j] = min(dp[i][k] + dp[k][j]) + C[i][j]인 경우
  2. 최적 분할점 k가 단조롭게 증가하는 경우 (Monotonicity)

이 최적화를 통해 시간 복잡도를 O(n³)에서 O(n²)로 줄일 수 있다.

기본적인 동적 계획법 문제

피보나치 수열(Fibonacci Sequence)

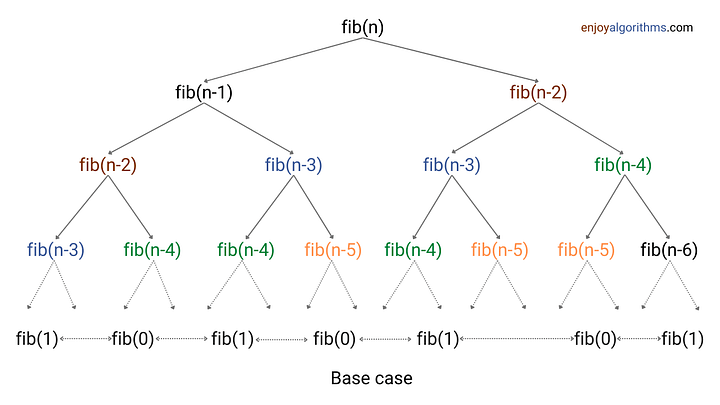
Dynamic Programming
Source: https://www.enjoyalgorithms.com/blog/introduction-to-dynamic-programming

하향식 접근법(메모이제이션):

1
2
3
4
5
6
7
8
9

def fibonacci_memoization(n, memo=None):
    if memo is None:
        memo = {0: 0, 1: 1}  # 기저 조건 초기화
    
    if n in memo:
        return memo[n]  # 이미 계산된 값이 있으면 반환
    
    memo[n] = fibonacci_memoization(n-1, memo) + fibonacci_memoization(n-2, memo)
    return memo[n]

상향식 접근법(테이블링):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def fibonacci_tabulation(n):
    if n <= 1:
        return n
    
    # 테이블 초기화
    dp = [0] * (n + 1)
    dp[1] = 1
    
    # 테이블 채우기
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    
    return dp[n]

최장 증가 부분 수열(Longest Increasing Subsequence, LIS)

주어진 수열에서 값이 증가하는 가장 긴 부분 수열의 길이를 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def longest_increasing_subsequence(nums):
    if not nums:
        return 0
    
    n = len(nums)
    dp = [1] * n  # 각 위치에서 끝나는 LIS의 길이
    
    for i in range(1, n):
        for j in range(i):
            if nums[i] > nums[j]:
                dp[i] = max(dp[i], dp[j] + 1)
    
    return max(dp)

상태 정의: dp[i]는 nums[i]를 마지막 원소로 하는 최장 증가 부분 수열의 길이 상태
전이 방정식: dp[i] = max(dp[i], dp[j] + 1) for all j < i where nums[i] > nums[j]

배낭 문제(Knapsack Problem)

배낭 문제는 주어진 용량의 배낭에 가치가 최대가 되도록 물건을 담는 문제.

0-1 배낭 문제:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def knapsack_01(weights, values, capacity):
    n = len(weights)
    dp = [[0 for _ in range(capacity + 1)] for _ in range(n + 1)]
    
    for i in range(1, n + 1):
        for w in range(capacity + 1):
            if weights[i-1] <= w:  # 현재 물건을 배낭에 넣을 수 있는 경우
                # 물건을 넣는 경우와 넣지 않는 경우 중 최대값 선택
                dp[i][w] = max(values[i-1] + dp[i-1][w-weights[i-1]], dp[i-1][w])
            else:  # 현재 물건을 배낭에 넣을 수 없는 경우
                dp[i][w] = dp[i-1][w]  # 이전 상태 그대로 유지
    
    return dp[n][capacity]

상태 정의: dp[i][w]는 처음 i개 물건과 용량 w인 배낭으로 얻을 수 있는 최대 가치 상태
전이 방정식:

편집 거리(Edit Distance)

두 문자열 사이의 최소 편집 거리를 계산하는 문제.
편집 연산은 삽입, 삭제, 대체를 포함.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def edit_distance(word1, word2):
    m, n = len(word1), len(word2)
    dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    
    # 기저 조건: 빈 문자열로 변환하는 경우
    for i in range(m + 1):
        dp[i][0] = i  # word1[:i]를 빈 문자열로 변환하려면 i번의 삭제 필요
    for j in range(n + 1):
        dp[0][j] = j  # 빈 문자열을 word2[:j]로 변환하려면 j번의 삽입 필요
    
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if word1[i-1] == word2[j-1]:  # 현재 문자가 같으면 편집 불필요
                dp[i][j] = dp[i-1][j-1]
            else:  # 현재 문자가 다르면 세 가지 연산 중 최소값 선택
                dp[i][j] = 1 + min(
                    dp[i-1][j],      # 삭제
                    dp[i][j-1],      # 삽입
                    dp[i-1][j-1]     # 대체
                )
    
    return dp[m][n]

상태 정의: dp[i][j]는 word1[:i]를 word2[:j]로 변환하는 데 필요한 최소 편집 거리 상태
전이 방정식:

동적 계획법의 분류와 패턴

문제 유형별 분류

  1. 최적화 문제(Optimization Problems): 최대값이나 최소값을 찾는 문제
    • 최대 합 경로(Maximum Sum Path)
    • 최소 비용 문제(Minimum Cost Problems)
  2. 계수 문제(Counting Problems): 특정 조건을 만족하는 방법의 수를 세는 문제
    • 계단 오르기(Climbing Stairs)
    • 조합의 수 계산(Combination Count)
  3. 결정 문제(Decision Problems): 특정 조건을 만족하는 해가 존재하는지 여부를 판단하는 문제
    • 부분 집합의 합(Subset Sum)
    • 문자열 매칭(String Matching)

차원에 따른 분류

  1. 1차원 DP: 상태가 하나의 변수로 표현되는 문제
    • 피보나치 수열
    • 최대 부분 배열 합(Maximum Subarray Sum)
  2. 2차원 DP: 상태가 두 개의 변수로 표현되는 문제
    • 배낭 문제
    • 최장 공통 부분 수열(Longest Common Subsequence)
  3. 다차원 DP: 상태가 세 개 이상의 변수로 표현되는 문제
    • 외판원 문제(Traveling Salesman Problem)의 특정 버전
    • 일부 그래프 관련 DP 문제

공통 패턴

  1. 구간 DP(Interval DP): 구간에 대한 연산을 다루는 문제
    • 행렬 곱셈 최적화(Matrix Chain Multiplication)
    • 최적 이진 검색 트리(Optimal Binary Search Tree)
  2. 경로 DP(Path DP): 그리드나 그래프에서 경로를 찾는 문제
    • 로봇 경로 계획(Robot Path Planning)
    • 최소 경로 합(Minimum Path Sum)
  3. 비트마스크 DP(Bitmask DP): 상태를 비트로 표현하는 문제
    • 외판원 문제(TSP)
    • 집합 커버링(Set Covering)
  4. 트리 DP(Tree DP): 트리 구조에서의 최적화 문제
    • 독립 집합(Independent Set) 문제
    • 트리 지름(Tree Diameter) 계산

동적 계획법의 한계 및 대안

  1. 문제의 한계
    동적 계획법이 효과적이지 않은 경우도 있다:
    1. 상태 공간이 너무 큰 경우: 상태 변수가 많거나 값의 범위가 넓으면 메모리 요구량이 과도해질 수 있다.
    2. 상태 전이 관계가 복잡한 경우: 하위 문제 간의 관계가 명확하지 않거나 복잡하면 DP 접근이 어려울 수 있다.
    3. 중복되는 하위 문제가 적은 경우: 중복이 적으면 메모이제이션의 이점이 줄어들어 분할 정복이 더 효율적일 수 있다.
    4. 그리디 접근이 최적인 경우: 일부 문제는 그리디 알고리즘으로 더 간단하고 효율적으로 해결할 수 있다.
  2. 대체 접근법
    동적 계획법의 한계를 극복하기 위한, 또는 특정 상황에서 더 적합할 수 있는 대안 접근법:
    1. 그리디 알고리즘(Greedy Algorithms): 각 단계에서 지역적으로 최적인 선택을 하는 방식으로, 일부 최적화 문제에서 효과적.
      • 예: 활동 선택 문제, 허프만 코딩
      1. 할 정복(Divide and Conquer)**: 중복되는 하위 문제가 적은 경우 더 효율적일 수 있다.
      • 예: 합병 정렬, 퀵 정렬
      1. 작위화 알고리즘(Randomized Algorithms)**: 확률적 요소를 도입하여 평균적으로 좋은 성능을 제공한다.
      • 예: 퀵 정렬의 무작위 피벗 선택
      1. 사 알고리즘(Approximation Algorithms)**: NP-난해 문제에 대해 근사적인 해를 효율적으로 찾는다.
      • 예: 여행자 문제의 2-근사 알고리즘
      1. 타휴리스틱(Metaheuristics)**: 복잡한 최적화 문제를 위한 일반적인 검색 전략이다.
      • 예: 유전 알고리즘, 시뮬레이티드 어닐링, 개미 군집 최적화
  3. 하이브리드 접근법
    여러 알고리즘 기법을 결합하여 각 접근법의 장점을 활용할 수 있다:
    1. DP + 그리디: 문제를 부분적으로는 DP로, 부분적으로는 그리디로 접근한다.
      • 예: 일부 스케줄링 문제
      1. P + 이진 검색**: 최적화 문제를 결정 문제로 변환하여 이진 검색으로 해결한다.
      • 예: 특정 파라미터화된 DP 문제
      1. P + 분할 정복**: 분할 정복으로 문제를 나누고 DP로 하위 문제를 해결한다.
      • 예: 일부 구간 DP 문제

실제 구현 및 최적화 기법

재귀와 반복적 구현 비교

동적 계획법은 재귀적(하향식) 또는 반복적(상향식) 방식으로 구현할 수 있으며, 각각 장단점이 있다:

재귀적 구현(하향식, 메모이제이션):

1
2
3
4
5
6
7
8
9

def fib_recursive(n, memo=None):
    if memo is None:
        memo = {}
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fib_recursive(n-1, memo) + fib_recursive(n-2, memo)
    return memo[n]

반복적 구현(상향식, 테이블링):

1
2
3
4
5
6
7
8

def fib_iterative(n):
    if n <= 1:
        return n
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

메모리 사용 최적화 기법

DP 구현에서 메모리 사용을 최적화하는 다양한 기법:

  1. 롤링 배열(Rolling Array): 이전 상태의 일부만 필요한 경우, 전체 테이블 대신 필요한 부분만 유지한다.

    1
2
3
4
5
6
7

    def fib_rolling_array(n):
    if n <= 1:
        return n
    a, b = 0, 1
    for i in range(2, n + 1):
        a, b = b, a + b
    return b

  2. 인접 상태만 저장: 직전 상태만 필요한 2차원 DP 문제에서 공간을 줄일 수 있다.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

    def min_path_sum_optimized(grid):
    if not grid or not grid[0]:
        return 0

    m, n = len(grid), len(grid[0])
    dp = [0] * n

    # 첫 번째 행 초기화
    dp[0] = grid[0][0]
    for j in range(1, n):
        dp[j] = dp[j-1] + grid[0][j]

    # 나머지 행 처리
    for i in range(1, m):
        dp[0] += grid[i][0]  # 첫 번째 열 업데이트
        for j in range(1, n):
            dp[j] = min(dp[j], dp[j-1]) + grid[i][j]

    return dp[n-1]

  3. 희소 테이블(Sparse Table): 모든 상태가 아닌 필요한 상태만 해시 맵에 저장한다.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

    def edit_distance_sparse(word1, word2):
    def dp(i, j, memo={}):
        if (i, j) in memo:
            return memo[(i, j)]
        if i == 0:
            return j
        if j == 0:
            return i

        if word1[i-1] == word2[j-1]:
            memo[(i, j)] = dp(i-1, j-1, memo)
        else:
            memo[(i, j)] = 1 + min(dp(i-1, j, memo), dp(i, j-1, memo), dp(i-1, j-1, memo))

        return memo[(i, j)]

    return dp(len(word1), len(word2))

병렬화 및 분산 계산

대규모 DP 문제에서 계산을 가속화하기 위한 기법:

  1. 단계별 병렬화: 같은 단계의 상태는 서로 독립적으로 계산할 수 있다.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

    def parallel_dp_example(n, num_threads=4):
    import concurrent.futures

    dp = [0] * (n + 1)
    dp[0] = 1  # 기저 조건

    # 각 단계별로 병렬 계산
    for i in range(1, n + 1):
        # 이 단계에서 계산해야 할 상태들
        states = get_states(i)  # 문제에 따라 다름

        with concurrent.futures.ThreadPoolExecutor(max_workers=num_threads) as executor:
            # 각 상태를 병렬로 계산
            future_to_state = {executor.submit(compute_state, j, dp): j for j in states}

            for future in concurrent.futures.as_completed(future_to_state):
                state = future_to_state[future]
                try:
                    dp[state] = future.result()
                except Exception as exc:
                    print(f'상태 {state} 계산 중 오류: {exc}')

    return dp[n]

  2. GPU 가속: 행렬 연산이 많은 DP 문제는 GPU를 활용하여 가속화할 수 있다.

  3. 맵리듀스(MapReduce): 대규모 DP 문제를 분산 환경에서 해결할 수 있다.
    이러한 병렬화 기법은 상태 간 의존성이 적은 문제에서 특히 효과적이다.

중급 동적 계획법 문제

최장 공통 부분 수열(Longest Common Subsequence, LCS)

두 문자열에서 순서가 유지되는 가장 긴 공통 부분 수열의 길이를 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def longest_common_subsequence(text1, text2):
    m, n = len(text1), len(text2)
    dp = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if text1[i-1] == text2[j-1]:
                dp[i][j] = dp[i-1][j-1] + 1
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
    
    return dp[m][n]

상태 정의: dp[i][j]는 text1[:i]와 text2[:j]의 최장 공통 부분 수열의 길이
상태 전이 방정식:

최대 부분 배열 합(Maximum Subarray Sum)

연속된 부분 배열 중 합이 최대인 부분 배열의 합을 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def maximum_subarray(nums):
    if not nums:
        return 0
    
    n = len(nums)
    dp = [0] * n  # dp[i]는 nums[i]로 끝나는 최대 부분 배열 합
    dp[0] = nums[0]
    
    for i in range(1, n):
        dp[i] = max(nums[i], dp[i-1] + nums[i])
    
    return max(dp)

상태 정의: dp[i]는 nums[i]를 마지막 원소로 포함하는 최대 부분 배열 합
상태 전이 방정식: dp[i] = max(nums[i], dp[i-1] + nums[i])

동전 교환 문제(Coin Change)

주어진 금액을 만들기 위해 필요한 최소한의 동전 개수를 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def coin_change(coins, amount):
    # dp[i]는 금액 i를 만드는 데 필요한 최소 동전 개수
    dp = [float('inf')] * (amount + 1)
    dp[0] = 0  # 금액 0은 동전 0개로 만들 수 있음
    
    for coin in coins:
        for i in range(coin, amount + 1):
            dp[i] = min(dp[i], dp[i - coin] + 1)
    
    return dp[amount] if dp[amount] != float('inf') else -1

상태 정의: dp[i]는 금액 i를 만드는 데 필요한 최소 동전 개수
상태 전이 방정식: dp[i] = min(dp[i], dp[i - coin] + 1) for all available coins

행렬 경로 문제(Matrix Path Problems)

그리드에서 특정 시작점에서 목표점까지의 최적 경로를 찾는 문제.

최소 경로 합(Minimum Path Sum):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def min_path_sum(grid):
    if not grid or not grid[0]:
        return 0
    
    m, n = len(grid), len(grid[0])
    dp = [[0 for _ in range(n)] for _ in range(m)]
    dp[0][0] = grid[0][0]
    
    # 첫 번째 행 초기화
    for j in range(1, n):
        dp[0][j] = dp[0][j-1] + grid[0][j]
    
    # 첫 번째 열 초기화
    for i in range(1, m):
        dp[i][0] = dp[i-1][0] + grid[i][0]
    
    # 나머지 셀 채우기
    for i in range(1, m):
        for j in range(1, n):
            dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
    
    return dp[m-1][n-1]

상태 정의: dp[i][j]는 (0,0)에서 (i,j)까지의 최소 경로 합
상태 전이 방정식: dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]

고급 동적 계획법 기법

상태 압축(State Compression)

상태를 비트로 표현하여 메모리 사용량을 줄이는 기법.
특히 집합을 다루는 문제에서 유용하다.

외판원 문제(TSP)의 DP 접근법:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def traveling_salesman(distances):
    n = len(distances)
    # dp[mask][i]는 방문한 도시 집합이 mask이고 현재 도시가 i일 때의 최소 거리
    dp = [[float('inf') for _ in range(n)] for _ in range(1 << n)]
    
    # 시작 도시는 0으로 가정
    dp[1][0] = 0  # 비트마스크 1은 0번 도시만 방문했음을 나타냄
    
    for mask in range(1, 1 << n):
        for i in range(n):
            # 현재 마스크에 i번 도시가 포함되어 있는지 확인
            if mask & (1 << i) == 0:
                continue
            
            # i번 도시를 마지막으로 방문했을 때의 이전 마스크
            prev_mask = mask & ~(1 << i)
            
            if prev_mask == 0:  # i가 시작 도시인 경우
                continue
            
            for j in range(n):
                if prev_mask & (1 << j):  # j번 도시가 이전에 방문되었는지 확인
                    dp[mask][i] = min(dp[mask][i], dp[prev_mask][j] + distances[j][i])
    
    # 모든 도시를 방문하고 0번 도시로 돌아오는 최소 거리
    return min(dp[(1 << n) - 1][i] + distances[i][0] for i in range(1, n))

확률적 DP(Probabilistic DP)

확률과 기대값을 다루는 문제에 DP를 적용하는 기법.

동전 던지기 기대값:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def expected_coin_flips(p_heads, target_heads):
    # dp[i]는 이미 i개의 앞면이 나왔을 때, 목표에 도달하기 위한 기대 던지기 횟수
    dp = [0] * (target_heads + 1)
    
    for i in range(target_heads - 1, -1, -1):
        # 다음 던지기에서 앞면이 나올 확률 p_heads
        # dp[i] = 1 (현재 던지기) + p_heads * dp[i+1] (앞면이 나온 경우) + (1-p_heads) * dp[i] (뒷면이 나온 경우)
        dp[i] = 1 + p_heads * dp[i+1] + (1-p_heads) * dp[i]
        dp[i] = (1 + p_heads * dp[i+1]) / p_heads
    
    return dp[0]

구간 DP(Interval DP)

특정 구간에 대한 연산을 최적화하는 문제에 적용되는 기법.

행렬 곱셈 최적화:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def matrix_chain_multiplication(dimensions):
    n = len(dimensions) - 1  # 행렬의 개수
    # dp[i][j]는 i번째 행렬부터 j번째 행렬까지 곱하는 데 필요한 최소 연산 수
    dp = [[0 for _ in range(n)] for _ in range(n)]
    
    for length in range(2, n + 1):  # 부분 체인의 길이
        for i in range(n - length + 1):
            j = i + length - 1
            dp[i][j] = float('inf')
            for k in range(i, j):  # i와 j 사이의 분할점
                operations = dp[i][k] + dp[k+1][j] + dimensions[i] * dimensions[k+1] * dimensions[j+1]
                dp[i][j] = min(dp[i][j], operations)
    
    return dp[0][n-1]

상태 정의: dp[i][j]는 i번째 행렬부터 j번째 행렬까지 곱하는 데 필요한 최소 연산 수
상태 전이 방정식: dp[i][j] = min(dp[i][k] + dp[k+1][j] + dimensions[i] * dimensions[k+1] * dimensions[j+1]) for all k in range(i, j)

결정적 DP(Decision DP)

최적의 결정 또는 선택 시퀀스를 찾는 문제에 적용되는 기법.

최적 이진 검색 트리:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def optimal_bst(keys, freq):
    n = len(keys)
    # dp[i][j]는 keys[i:j+1]로 구성된 최적 BST의 기대 탐색 비용
    dp = [[0 for _ in range(n)] for _ in range(n)]
    
    # 길이 1인 부분 키 배열에 대한 초기화
    for i in range(n):
        dp[i][i] = freq[i]
    
    for length in range(2, n + 1):  # 부분 배열의 길이
        for i in range(n - length + 1):
            j = i + length - 1
            dp[i][j] = float('inf')
            
            # 구간 합 계산
            freq_sum = sum(freq[i:j+1])
            
            for r in range(i, j + 1):  # i부터 j까지의 모든 키를 루트로 시도
                left_cost = dp[i][r-1] if r > i else 0
                right_cost = dp[r+1][j] if r < j else 0
                dp[i][j] = min(dp[i][j], left_cost + right_cost + freq_sum)
    
    return dp[0][n-1]

실제 응용 사례 및 문제

문자열 처리 문제

팰린드롬 부분 문자열

가장 긴 팰린드롬 부분 문자열을 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

def longest_palindromic_substring(s):
    if not s:
        return ""
    
    n = len(s)
    # dp[i][j]는 s[i:j+1]이 팰린드롬인지 여부
    dp = [[False for _ in range(n)] for _ in range(n)]
    
    start, max_len = 0, 1
    
    # 모든 길이 1인 부분 문자열은 팰린드롬
    for i in range(n):
        dp[i][i] = True
    
    # 길이 2인 부분 문자열 검사
    for i in range(n - 1):
        if s[i] == s[i + 1]:
            dp[i][i + 1] = True
            start = i
            max_len = 2
    
    # 길이 3 이상인 부분 문자열 검사
    for length in range(3, n + 1):
        for i in range(n - length + 1):
            j = i + length - 1
            if s[i] == s[j] and dp[i + 1][j - 1]:
                dp[i][j] = True
                start = i
                max_len = length
    
    return s[start:start + max_len]

상태 정의: dp[i][j]는 s[i:j+1]이 팰린드롬인지 여부
상태 전이 방정식: dp[i][j] = (s[i] == s[j]) and dp[i+1][j-1]

정규 표현식 매칭

문자열이 주어진 패턴과 매칭되는지 확인하는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

def is_match(s, p):
    m, n = len(s), len(p)
    # dp[i][j]는 s[:i]와 p[:j]가 매칭되는지 여부
    dp = [[False for _ in range(n + 1)] for _ in range(m + 1)]
    
    # 빈 문자열과 빈 패턴은 매칭됨
    dp[0][0] = True
    
    # 빈 문자열과 패턴의 매칭 처리 (패턴이 a*b*c* 형태인 경우)
    for j in range(1, n + 1):
        if p[j - 1] == '*':
            dp[0][j] = dp[0][j - 2]
    
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if p[j - 1] == '*':
                # 패턴의 이전 문자를 0번 사용하는 경우
                dp[i][j] = dp[i][j - 2]
                
                # 패턴의 이전 문자를 1번 이상 사용하는 경우
                if p[j - 2] == '.' or p[j - 2] == s[i - 1]:
                    dp[i][j] = dp[i][j] or dp[i - 1][j]
            elif p[j - 1] == '.' or p[j - 1] == s[i - 1]:
                dp[i][j] = dp[i - 1][j - 1]
    
    return dp[m][n]

상태 정의: dp[i][j]는 s[:i]와 p[:j]가 매칭되는지 여부
상태 전이 방정식은 패턴의 현재 문자에 따라 다르다.

그래프 문제

최단 경로 문제

플로이드-워셜(Floyd-Warshall) 알고리즘은 모든 정점 쌍 간의 최단 경로를 찾는 DP 기반 알고리즘이다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def floyd_warshall(graph):
    n = len(graph)
    dist = [row[:] for row in graph]  # 그래프의 인접 행렬 복사
    
    # 각 정점을 중간 정점으로 고려
    for k in range(n):
        # 모든 정점 쌍에 대해
        for i in range(n):
            for j in range(n):
                # i에서 k를 거쳐 j로 가는 경로가 더 짧은지 확인
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]
    
    return dist

상태 정의: dist[i][j]는 정점 i에서 j까지의 최단 거리
상태 전이 방정식: dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

최장 경로 문제

유향 비순환 그래프(DAG)에서의 최장 경로 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

def longest_path_in_dag(graph, n):
    # 위상 정렬
    in_degree = [0] * n
    for i in range(n):
        for j, _ in graph[i]:
            in_degree[j] += 1
    
    queue = [i for i in range(n) if in_degree[i] == 0]
    topo_order = []
    
    while queue:
        u = queue.pop(0)
        topo_order.append(u)
        for v, _ in graph[u]:
            in_degree[v] -= 1
            if in_degree[v] == 0:
                queue.append(v)
    
    # 최장 경로 계산
    dist = [float('-inf')] * n
    for i in range(n):
        if in_degree[i] == 0:  # 시작점
            dist[i] = 0
    
    for u in topo_order:
        for v, weight in graph[u]:
            if dist[v] < dist[u] + weight:
                dist[v] = dist[u] + weight
    
    return max(dist)

상태 정의: dist[i]는 시작점에서 정점 i까지의 최장 경로 길이
상태 전이 방정식: dist[v] = max(dist[v], dist[u] + weight) for all edges (u,v)

게임 이론 문제

님 게임(Nim Game)

여러 개의 돌 더미에서 번갈아가며 돌을 가져가는 님 게임의 승자를 결정하는 문제.

1
2
3
4
5
6
7

def can_win_nim(piles):
    # XOR 합이 0이 아니면 첫 번째 플레이어가 이길 수 있음
    xor_sum = 0
    for pile in piles:
        xor_sum ^= pile
    
    return xor_sum != 0

이 문제는 스프라그-그런디 정리(Sprague-Grundy Theorem)를 사용하여 해결할 수 있다.

돌 게임(Stone Game)

두 플레이어가 번갈아가며 양끝에서 돌을 가져가는 게임에서 최적의 전략을 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

def stone_game(piles):
    n = len(piles)
    # dp[i][j]는 piles[i:j+1]에서 선공이 후공보다 얼마나 많이 가져갈 수 있는지
    dp = [[0 for _ in range(n)] for _ in range(n)]
    
    # 기저 조건: 돌이 하나만 있는 경우
    for i in range(n):
        dp[i][i] = piles[i]
    
    for length in range(2, n + 1):
        for i in range(n - length + 1):
            j = i + length - 1
            # 선공이 왼쪽(piles[i]) 또는 오른쪽(piles[j])을 선택한 후,
            # 새로운 게임에서는 선공과 후공의 역할이 바뀜
            dp[i][j] = max(piles[i] - dp[i+1][j], piles[j] - dp[i][j-1])
    
    return dp[0][n-1] > 0  # 선공이 이길 수 있는지 여부

상태 정의: dp[i][j]는 piles[i:j+1]에서 선공이 후공보다 얼마나 많이 가져갈 수 있는지
상태 전이 방정식: dp[i][j] = max(piles[i] - dp[i+1][j], piles[j] - dp[i][j-1])

확률 및 기대값 문제

주식 거래 최적 시점(Best Time to Buy and Sell Stock)

주식 가격 배열이 주어졌을 때, 최대 이익을 얻을 수 있는 거래 방법을 찾는 문제.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def max_profit(prices):
    if not prices:
        return 0
    
    n = len(prices)
    # dp[i][j]는 i일에 j상태일 때의 최대 이익 (j: 0=현금 보유, 1=주식 보유)
    dp = [[0, 0] for _ in range(n)]
    
    # 기저 조건
    dp[0][0] = 0  # 0일에 현금 보유
    dp[0][1] = -prices[0]  # 0일에 주식 구매
    
    for i in range(1, n):
        # 현금 보유: 전날 현금 그대로 또는 전날 주식 팔기
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        # 주식 보유: 전날 주식 그대로 또는 전날 현금으로 주식 구매
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
    
    # 마지막 날에는 현금을 갖고 있는 것이 최적
    return dp[n-1][0]

상태 정의: dp[i][j]는 i일에 j상태일 때의 최대 이익
상태 전이 방정식:

최근 연구 및 동향

  1. 강화 학습과의 연관성
    동적 계획법은 강화 학습의 이론적 기반을 제공한다:
    1. 벨만 방정식(Bellman Equation): 강화 학습의 핵심인 벨만 방정식은 동적 계획법의 원리에 기반한다.
    2. 가치 반복(Value Iteration)과 정책 반복(Policy Iteration): 이 두 알고리즘은 마르코프 결정 과정(MDP)에서 최적 정책을 찾기 위한 DP 기반 방법이다.
    3. Q-learning과 SARSA: 이러한 모델 프리(model-free) 강화 학습 알고리즘도 DP의 개념을 확장한 것이다.
    4. 심층 강화 학습(Deep Reinforcement Learning): DQN(Deep Q-Network)과 같은 알고리즘은 신경망을 사용하여 DP의 한계를 극복한다.
  2. 근사 동적 계획법(Approximate Dynamic Programming)
    대규모 상태 공간을 다루기 위한 DP의 확장:
    1. 함수 근사기(Function Approximation): 모든 상태의 값을 저장하는 대신, 함수(예: 신경망)를 사용하여 값을 근사한다.
    2. 차원 축소(Dimensionality Reduction): 고차원 상태 공간을 저차원으로 매핑하여 다루기 쉽게 만든다.
    3. 시뮬레이션 기반 최적화(Simulation-Based Optimization): 몬테카를로 시뮬레이션을 사용하여 상태 값을 추정한다.
    4. 시간차 학습(Temporal Difference Learning): 샘플 기반 방법으로 벨만 방정식을 근사적으로 해결한다.
  3. 메타 동적 계획법(Meta Dynamic Programming)
    동적 계획법 자체를 최적화하거나 자동화하는 연구:
    1. 자동 상태 설계(Automatic State Design): 문제에 맞는 최적의 상태 표현을 자동으로 찾는다.
    2. 알고리즘 포트폴리오(Algorithm Portfolios): 여러 DP 알고리즘을 조합하여 문제에 맞게 적용한다.
    3. 하이퍼파라미터 최적화(Hyperparameter Optimization): DP 알고리즘의 파라미터를 자동으로 튜닝한다.
    4. 신경 동적 계획법(Neural Dynamic Programming): 신경망과 DP를 결합하여 복잡한 구조적 예측 문제를 해결한다.

참고 및 출처