분할 정복 (Divide and Conquer)

분할 정복 (Divide and Conquer)

분할 정복은 알고리즘 설계에서 가장 강력하고 널리 사용되는 패러다임 중 하나이다.
복잡한 문제를 더 작고 관리하기 쉬운 하위 문제들로 나누어 해결하는 이 접근법은 효율적인 알고리즘 설계의 핵심 원리이다.

정의와 원리

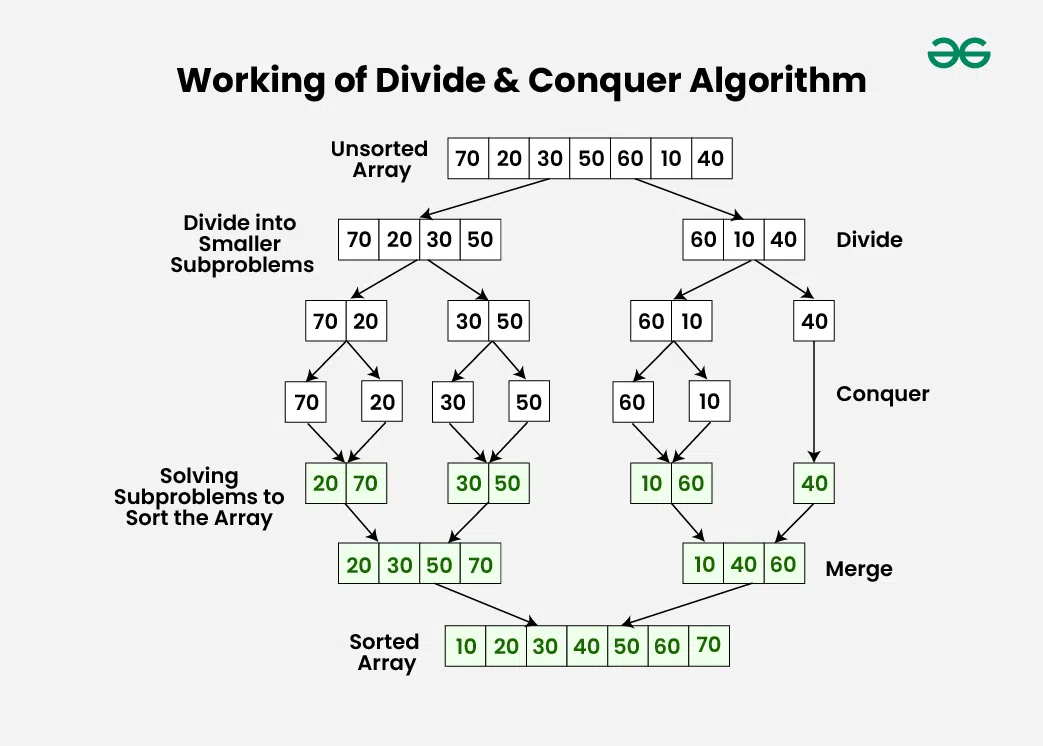
분할 정복(Divide and Conquer)은 복잡한 문제를 다음과 같은 세 단계로 해결하는 알고리즘 설계 기법이다:

1. 분할(Divide): 원래 문제를 같은 유형의 더 작은 하위 문제들로 나눈다.
2. 정복(Conquer): 하위 문제들을 재귀적으로 해결한다. 하위 문제가 충분히 작으면 직접 해결한다.
3. 결합(Combine): 하위 문제들의 해결책을 결합하여 원래 문제의 해결책을 만든다.

분할 정복은 재귀적 사고에 기반하며, 큰 문제를 동일한 형태의 작은 문제들로 축소하여 해결하는 방식이다.
이 과정은 문제가 충분히 작아질 때까지 계속된다.

1. 분할(Divide)

분할 단계는 원래 문제를 더 작은 하위 문제들로 나누는 과정이다.
이 단계에서는 다음과 같은 중요한 고려사항들이 있다:

분할의 핵심 원칙

• 크기 축소: 각 하위 문제는 원래 문제보다 규모가 작아야 한다. 이는 재귀적 접근의 핵심으로, 종료 조건에 도달할 수 있게 한다.
• 유형 유지: 하위 문제들은 원래 문제와 동일한 형태여야 한다. 이렇게 하면 같은 알고리즘을 재귀적으로 적용할 수 있다.
• 독립성: 이상적으로는, 하위 문제들이 서로 독립적이어야 효율적인 병렬 처리가 가능하다.

분할 전략의 종류

• 균등 분할: 문제를 거의 동일한 크기의 하위 문제들로 나눈다(예: 머지 소트에서 배열을 반으로 나누기).
• 불균등 분할: 문제를 다양한 크기의 하위 문제들로 나눈다(예: 퀵 소트에서 피벗을 기준으로 나누기).
• 차원 감소: 다차원 문제를 더 낮은 차원의 문제로 변환한다(예: 스트라센 행렬 곱셈 알고리즘).

2. 정복(Conquer)

정복 단계에서는 나누어진 하위 문제들을 해결한다.
분할된 문제가 충분히 작으면 직접 해결하고, 그렇지 않으면 재귀적으로 분할 정복 알고리즘을 적용한다.

정복의 핵심 원칙

• 기저 사례(Base Case) 처리: 더 이상 나눌 수 없는 가장 작은 하위 문제에 도달했을 때의 해결 방법을 정의한다.
• 재귀적 해결: 기저 사례가 아니면, 같은 알고리즘을 하위 문제에 재귀적으로 적용한다.
• 독립적 해결: 각 하위 문제는 다른 하위 문제의 해결에 영향을 주지 않고 독립적으로 해결된다.

정복 과정의 특징

• 깊이 우선 탐색: 재귀 호출을 통해 문제 해결이 깊이 우선으로 진행된다.
• 병렬화 가능성: 독립적인 하위 문제들은 병렬로 처리될 수 있어 다중 프로세서 환경에서 효율성을 높일 수 있다.
• 메모리 사용: 재귀 호출 스택으로 인해 일정 수준의 메모리 오버헤드가 발생한다.

3. 결합(Combine)

결합 단계에서는 하위 문제들의 해결책을 통합하여 원래 문제의 해결책을 만든다.
이 단계는 분할 정복 알고리즘의 효율성과 정확성에 중요한 영향을 미친다.

결합의 핵심 원칙

• 효율적 통합: 하위 문제들의 해결책을 효율적으로 결합하는 방법이 중요하다.
• 전체 최적성 보장: 결합 과정이 하위 문제 해결책들을 결합하여 전체 문제의 최적해를 제공해야 한다.
• 정보 보존: 하위 문제의 해결책을 결합할 때 중요한 정보가 손실되지 않아야 한다.

결합 방법의 종류

• 단순 결합: 하위 문제의 해결책을 직접 이어 붙이는 방식(예: 배열 연결).
• 병합 결합: 두 개 이상의 정렬된 하위 문제 해결책을 병합하는 방식(예: 머지 소트의 병합 단계).
• 수학적 결합: 하위 문제의 해결책에 수학적 연산을 적용하는 방식(예: 카라츠바 알고리즘의 곱셈 결과 결합).
• 선택적 결합: 하위 문제 해결책 중 조건에 맞는 것만 선택하는 방식(예: 최댓값/최솟값 찾기).

분할 정복의 세 단계가 함께 작동하는 방식

세 단계는 서로 밀접하게 연결되어 전체 알고리즘의 성능과 정확성을 결정한다:

1. 분할 단계에서 문제를 얼마나 효과적으로 나누는지가 알고리즘의 깊이와 효율성에 영향을 미친다.
2. 정복 단계에서 기저 사례의 선택과 재귀적 해결 방식이 알고리즘의 정확성을 보장한다.
3. 결합 단계의 효율성이 전체 알고리즘의 시간 복잡도에 중요한 영향을 미친다.

분할 정복의 특징

분할 정복 알고리즘의 주요 특징은 다음과 같다:

• 재귀적 구조: 대부분의 분할 정복 알고리즘은 재귀 함수로 구현된다.
• 하위 문제의 독립성: 보통 하위 문제들은 서로 독립적이어야 효율적이다.
• 베이스 케이스: 재귀의 종료 조건으로, 더 이상 분할할 수 없는 가장 작은 문제이다.
• 최적 부분 구조: 큰 문제의 최적해가 하위 문제들의 최적해로부터 구성된다.

분할 정복 알고리즘 설계 방법론

1. 문제 분석 및 분할 전략
   효과적인 분할 정복 알고리즘을 설계하기 위한 단계:
   1. 문제의 재귀적 구조 파악: 문제가 어떻게 더 작은 동일 유형의 하위 문제로 나눠질 수 있는지 분석한다.
   2. 분할 지점 선택: 문제를 어떤 기준으로 분할할지 결정한다(예: 배열의 중간, 특정 피벗 등).
   3. 독립성 확인: 하위 문제들이 독립적으로 해결 가능한지 확인한다.
   4. 베이스 케이스 정의: 재귀의 종료 조건이 될 가장 작은 문제 크기를 결정한다.
   5. 결합 방법 설계: 하위 문제의 해결책들을 어떻게 결합하여 원래 문제의 해결책을 만들지 결정한다.
2. 알고리즘 분석 및 최적화
   분할 정복 알고리즘의 성능을 분석하고 최적화하는 방법:
   1. 재귀 관계식 도출: T(n) = aT(n/b) + f(n) 형태의 관계식을 세운다.
   2. 마스터 정리 적용: 시간 복잡도의 점근적 상한을 결정한다.
   3. 병목 지점 식별: 알고리즘에서 가장 비용이 많이 드는 부분을 찾는다.
   4. 분할 균형성 평가: 분할이 얼마나 균형잡혀 있는지 분석한다.
   5. 하이브리드 접근법 고려: 다른 알고리즘 패러다임과의 결합 가능성을 탐색한다.
3. 재귀 구현 최적화
   재귀적으로 구현된 분할 정복 알고리즘의 성능을 향상시키는 기법:
   1. 꼬리 재귀 최적화: 재귀 호출이 함수의 마지막 연산인 경우, 컴파일러가 이를 반복문으로 최적화할 수 있다.
   2. 메모이제이션 적용: 이미 계산된 하위 문제의 결과를 저장하여 재계산을 방지한다.
   3. 하위 문제 크기 최적화: 작은 하위 문제는 재귀 대신 직접적인 방법으로 해결한다.
   4. 스택 메모리 관리: 깊은 재귀를 피하고 스택 오버플로를 방지하는 전략을 적용한다.
4. 병렬 구현 전략
   분할 정복 알고리즘을 효과적으로 병렬화하는 방법:
   1. 작업 크기 조정: 병렬화할 가치가 있는 최소 하위 문제 크기를 결정한다.
   2. 작업 풀 관리: 스레드 풀을 사용하여 스레드 생성 오버헤드를 줄인다.
   3. 로드 밸런싱: 작업 훔치기(work stealing) 등의 기법으로 프로세서 간 부하를 균등하게 분배한다.
   4. 동기화 최소화: 불필요한 동기화를 줄여 병렬 효율성을 높인다.
   5. 메모리 지역성 고려: 캐시 효율성을 높이는 메모리 접근 패턴을 설계한다.

분할 정복의 수학적 분석

1. 시간 복잡도 분석
   분할 정복 알고리즘의 시간 복잡도는 주로 마스터 정리(Master Theorem)를 사용하여 분석된다.
   일반적인 재귀 관계식은 다음과 같다:
   T(n) = aT(n/b) + f(n)
   여기서:

   • T(n)은 크기가 n인 문제를 해결하는 데 필요한 시간
   • a는 생성되는 하위 문제의 수
   • b는 하위 문제의 크기가 얼마나 감소하는지를 나타내는 요소
   • f(n)은 분할과 결합 단계에 드는 추가 작업의 비용

   마스터 정리는 이 재귀 관계식을 n의 함수로 표현된 폐쇄형(closed form)으로 해결한다.

2. 공간 복잡도 분석
   분할 정복 알고리즘의 공간 복잡도는 주로 재귀 호출 스택의 깊이와 각 단계에서 필요한 추가 공간에 의해 결정된다. 일반적으로 다음과 같은 요소를 고려한다:

   • 재귀 호출 스택의 최대 깊이
   • 각 재귀 호출에서 필요한 추가 메모리
   • 결과를 저장하기 위한 공간

3. 재귀 관계식 해결
   분할 정복 알고리즘의 성능을 분석하려면 재귀 관계식을 해결해야 한다.
   마스터 정리는 세 가지 경우로 분류된다:

   1. f(n) = O(n^c) 이고 c < log_b(a)인 경우: T(n) = Θ(n^(log_b(a)))
   2. f(n) = Θ(n^c) 이고 c = log_b(a)인 경우: T(n) = Θ(n^c * log n)
   3. f(n) = Ω(n^c) 이고 c > log_b(a)인 경우: T(n) = Θ(f(n))
      이 분류를 통해 많은 분할 정복 알고리즘의 복잡도를 쉽게 결정할 수 있다.

분할 정복의 구현 기법

재귀 구현 vs. 반복 구현

분할 정복 알고리즘은 대부분 자연스럽게 재귀적으로 구현되지만, 스택 오버플로를 방지하거나 성능을 개선하기 위해 반복적으로 구현할 수도 있다.

재귀 구현의 장단점:

• 장점: 알고리즘의 논리를 더 명확하게 표현할 수 있다.
• 단점: 함수 호출 오버헤드와 스택 오버플로 위험이 있다.

반복 구현의 장단점:

• 장점: 함수 호출 오버헤드가 없고 스택 오버플로 위험이 없다.
• 단점: 코드가 더 복잡해질 수 있다.

이진 검색의 반복 구현 예시:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def binary_search_iterative(arr, target):
    left, right = 0, len(arr) - 1
    
    while left <= right:
        mid = (left + right) // 2
        
        if arr[mid] == target:
            return mid
        elif arr[mid] > target:
            right = mid - 1
        else:
            left = mid + 1
    
    return -1  # 타겟을 찾지 못함

메모이제이션과의 결합

분할 정복 알고리즘이 중복된 하위 문제를 해결해야 할 경우, 동적 프로그래밍의 메모이제이션 기법을 결합하여 효율성을 크게 향상시킬 수 있다.

피보나치 수열 계산 예시:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def fibonacci(n, memo={}):
    # 메모이제이션을 활용한 분할 정복
    if n in memo:
        return memo[n]
    
    if n <= 1:
        return n
    
    memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
    return memo[n]

이 방식은 순수한 분할 정복(O(2^n))보다 훨씬 효율적인 O(n) 시간 복잡도를 제공한다.

병렬 처리와 분할 정복

분할 정복 알고리즘은 본질적으로 병렬화에 적합하다.
독립적인 하위 문제들을 서로 다른 프로세서나 스레드에서 동시에 처리할 수 있기 때문이다.

병렬 병합 정렬 개념:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

def parallel_merge_sort(arr, num_threads=4):
    if len(arr) <= 1:
        return arr
    
    # 충분히 작은 배열에 대해서는 일반 병합 정렬 사용
    if len(arr) < 1000 or num_threads <= 1:
        return merge_sort(arr)
    
    mid = len(arr) // 2
    
    # 두 하위 문제를 병렬로 처리
    import concurrent.futures
    with concurrent.futures.ThreadPoolExecutor() as executor:
        left_future = executor.submit(parallel_merge_sort, arr[:mid], num_threads // 2)
        right = parallel_merge_sort(arr[mid:], num_threads // 2)
        left = left_future.result()
    
    # 결과 병합
    return merge(left, right)

실제 구현에서는 스레드 생성 오버헤드와 병렬화 이득 사이의 균형을 고려해야 한다.

분할 정복의 최적화 기법

분할 정복 알고리즘의 성능을 향상시키는 다양한 최적화 기법이 있다:

1. 하위 문제 크기 최적화: 작은 크기의 하위 문제에 대해서는 더 단순하고 효율적인 알고리즘 사용
2. 균형 잡힌 분할: 가능한 한 균등하게 문제를 분할하여 최악의 경우 성능 개선
3. 캐시 효율성 고려: 메모리 접근 패턴을 최적화하여 캐시 적중률 향상
4. 데이터 구조 선택: 문제에 적합한 데이터 구조를 사용하여 연산 효율성 증가
5. 하드웨어 최적화: SIMD(Single Instruction Multiple Data) 명령어 등을 활용한 하드웨어 수준 최적화

분할 정복의 고급 응용

1. 정렬 알고리즘의 확장
   병합 정렬의 변형:

   • 외부 정렬(External Sort): 메인 메모리에 담기 어려운 대용량 데이터를 정렬하는 기법으로, 분할 정복 원리를 확장한다.
   • 병렬 병합 정렬(Parallel Merge Sort): 여러 프로세서나 스레드를 활용하여 병합 정렬을 병렬화한다.

   퀵 정렬의 최적화:

   • 피벗 선택 전략: 중앙값의 중앙값(Median of Medians) 등의 방법으로 좋은 피벗을 선택하여 최악의 경우 성능을 개선한다.
   • 삽입 정렬 하이브리드: 작은 부분 배열에 대해서는 삽입 정렬을 사용하여 재귀 오버헤드를 줄인다.
   • 3-way 퀵 정렬: 동일한 값이 많은 경우 성능을 향상시키는 방법이다.

2. 계산 기하학에서의 응용

   • 가장 가까운 점 쌍 찾기(Closest Pair of Points): 분할 정복을 사용하여 2D 평면상의 n개 점들 중 가장 가까운 두 점을 O(n log n) 시간에 찾을 수 있다.
     • 알고리즘 개요:
       1. 점들을 x좌표에 따라 정렬한다.
       2. 점 집합을 중간에서 두 부분으로 나눈다.
       3. 각 부분에서 재귀적으로 가장 가까운 점 쌍을 찾는다.
       4. 두 부분에 걸쳐 있는(중간선 근처의) 점들 사이에서 가장 가까운 쌍을 찾는다.
       5. 세 경우 중 최소 거리를 반환한다.
   • 볼록 껍질(Convex Hull): 2D 점 집합의 볼록 껍질을 찾는 문제도 분할 정복 접근법을 사용할 수 있다.

3. FFT(Fast Fourier Transform)
   FFT는 신호 처리와 다항식 곱셈에 매우 중요한 알고리즘으로, 분할 정복의 원리를 사용한다.

   • 알고리즘 개요:
     1. 짝수 인덱스와 홀수 인덱스의 샘플로 신호를 분할한다.
     2. 각 부분에 대해 재귀적으로 FFT를 계산한다.
     3. 이 결과들을 결합하여 전체 FFT를 구성한다.

   FFT는 O(n log n) 시간 복잡도를 가지며, 이는 고전적인 O(n²) 방법보다 훨씬 효율적이다.

4. 정수 곱셈 알고리즘
   카라츠바 알고리즘(Karatsuba algorithm)은 큰 정수의 곱셈을 더 효율적으로 수행하는 분할 정복 알고리즘이다.

   • 알고리즘 개요: 두 n자리 수 x와 y가 있을 때:
     1. x = a × 10^(n/2) + b와 y = c × 10^(n/2) + d로 분할한다.
     2. x × y = (a × 10^(n/2) + b) × (c × 10^(n/2) + d) 로 표현된다.
     3. 이를 전개하는 대신, 3번의 곱셈(일반적인 방법은 4번 필요)만으로 계산한다:
        • ac = a × c
        • bd = b × d
        • (a+b)(c+d) = ac + bd + (ad + bc)에서 (ad + bc)를 계산한다.

   시간 복잡도:

   • 표준 곱셈: O(n²)
   • 카라츠바 알고리즘: O(n^log_2(3)) ≈ O(n^1.58)

분할 정복의 한계와 대안

1. 재귀적 오버헤드
   분할 정복 알고리즘의 재귀적 구현은 다음과 같은 오버헤드를 발생시킬 수 있다:

   • 함수 호출 스택 관리 비용
   • 스택 오버플로 위험
   • 캐시 지역성(cache locality) 저하 가능성
     대안 및 해결책:
   • 작은 크기의 입력에 대해서는 직접적인 방법 사용(하이브리드 접근법)
   • 꼬리 재귀(tail recursion) 최적화
   • 반복적 구현으로 전환

2. 분할 균형성 문제
   불균형한 분할은 분할 정복 알고리즘의 성능을 크게 저하시킬 수 있다.

   • 예시: 퀵 정렬에서 이미 정렬된 배열에 대해 항상 첫 번째 원소를 피벗으로 선택하면, 매 단계에서 n-1과 0으로 불균형하게 분할되어 O(n²) 시간이 소요된다.
   • 대안 및 해결책:
     • 랜덤 피벗 선택
     • 중앙값의 중앙값 알고리즘을 통한 좋은 피벗 선택
     • 다양한 피벗 선택 전략(첫 번째, 중간, 마지막 원소의 중앙값 등)

3. 메모리 사용량
   일부 분할 정복 알고리즘은 상당한 메모리를 필요로 한다:

   • 재귀 호출 스택에 필요한 메모리
   • 합병 정렬과 같은 알고리즘에서 추가 배열에 필요한 메모리
   • 대안 및 해결책:
     • 제자리 정렬 알고리즘(in-place sorting algorithms) 사용
     • 반복적 구현으로 스택 메모리 사용 감소
     • 외부 정렬(external sorting) 기법 적용

4. 병렬화의 어려움
   이론적으로 분할 정복은 병렬화에 적합하지만, 실제로는 다음과 같은 어려움이 있을 수 있다:

   • 작업 분배의 불균형
   • 스레드/프로세스 생성 및 관리 오버헤드
   • 결합 단계에서의 동기화 비용
   • 대안 및 해결책:
     • 작업 훔치기(work stealing) 스케줄링
     • 균형 잡힌 분할을 위한 전처리
     • 일정 크기 이하의 하위 문제는 순차적으로 처리

대표적인 분할 정복 알고리즘

합병 정렬(Merge Sort)

합병 정렬은 분할 정복 패러다임을 잘 보여주는 대표적인 정렬 알고리즘이다.

알고리즘 개요:

1. 분할: 배열을 중간에서 두 부분으로 나눈다.
2. 정복: 두 부분 배열을 재귀적으로 정렬한다.
3. 결합: 정렬된 두 부분 배열을 합병하여 하나의 정렬된 배열을 만든다.

Python 구현:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

def merge_sort(arr):
    # 베이스 케이스: 배열의 길이가 1 이하면 이미 정렬된 것으로 간주
    if len(arr) <= 1:
        return arr
    
    # 분할 단계: 배열을 중간에서 두 부분으로 나눔
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]
    
    # 정복 단계: 두 부분 배열을 재귀적으로 정렬
    left = merge_sort(left)
    right = merge_sort(right)
    
    # 결합 단계: 정렬된 두 부분 배열을 합병
    return merge(left, right)

def merge(left, right):
    result = []
    i = j = 0
    
    # 두 배열의 요소를 비교하여 작은 것부터 결과 배열에 추가
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    
    # 남은 요소들을 결과 배열에 추가
    result.extend(left[i:])
    result.extend(right[j:])
    
    return result

시간 복잡도:

• 최악 및 평균 케이스: O(n log n)
• 최선 케이스: O(n log n)

공간 복잡도: O(n)

합병 정렬의 주요 장점은 안정적인 정렬이며 최악의 경우에도 O(n log n)의 성능을 보장한다는 점이다.
단점은 추가 메모리가 필요하다는 것이다.

퀵 정렬(Quick Sort)

퀵 정렬은 평균적으로 매우 효율적인 분할 정복 정렬 알고리즘이다.

알고리즘 개요:

1. 분할: 피벗을 선택하고 배열을 피벗보다 작은 요소들과 큰 요소들로 분할한다.
2. 정복: 분할된 두 부분 배열을 재귀적으로 정렬한다.
3. 결합: 정렬된 부분 배열들은 이미 전체 배열의 순서에 맞게 있으므로 별도의 결합 과정이 필요 없다.

Python 구현:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    
    pivot = arr[len(arr) // 2]  # 피벗 선택 (중간 요소)
    left = [x for x in arr if x < pivot]  # 피벗보다 작은 요소들
    middle = [x for x in arr if x == pivot]  # 피벗과 같은 요소들
    right = [x for x in arr if x > pivot]  # 피벗보다 큰 요소들
    
    # 분할된 부분 배열들을 재귀적으로 정렬하고 결합
    return quick_sort(left) + middle + quick_sort(right)

시간 복잡도:

• 최선 및 평균 케이스: O(n log n)
• 최악 케이스: O(n²) (이미 정렬된 배열이나 역순으로 정렬된 배열에서 발생)

공간 복잡도:

• 평균: O(log n) (재귀 호출 스택)
• 최악: O(n)

퀵 정렬의 주요 장점은 평균적으로 매우 빠르고 추가 메모리가 적게 필요하다는 점이다.
단점은 최악의 경우 O(n²)의 시간 복잡도를 가질 수 있다는 것이다.

이진 검색(Binary Search)

이진 검색은 정렬된 배열에서 특정 요소의 위치를 찾는 효율적인 알고리즘이다.

알고리즘 개요:

1. 분할: 배열의 중간 요소를 확인하고, 찾고자 하는 값과 비교한다.
2. 정복: 찾고자 하는 값이 중간 요소보다 작으면 왼쪽 절반을, 크면 오른쪽 절반을 재귀적으로 검색한다.
3. 결합: 이진 검색에서는 별도의 결합 단계가 필요 없다.

Python 구현:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def binary_search(arr, target, left=0, right=None):
    if right is None:
        right = len(arr) - 1
    
    # 베이스 케이스: 검색 범위가 비어 있으면 타겟이 없음
    if left > right:
        return -1
    
    # 중간 인덱스 계산
    mid = (left + right) // 2
    
    # 중간 요소와 타겟 비교
    if arr[mid] == target:
        return mid  # 타겟을 찾음
    elif arr[mid] > target:
        # 타겟이 중간 요소보다 작으면 왼쪽 절반 검색
        return binary_search(arr, target, left, mid - 1)
    else:
        # 타겟이 중간 요소보다 크면 오른쪽 절반 검색
        return binary_search(arr, target, mid + 1, right)

시간 복잡도: O(log n)

공간 복잡도:

• 재귀 구현: O(log n) (재귀 호출 스택)
• 반복 구현: O(1)

이진 검색의 주요 장점은 매우 효율적인 O(log n) 시간 복잡도이다.
그러나 배열이 정렬되어 있어야 한다는 전제 조건이 있다.

최대 부분 배열 문제(Maximum Subarray Problem)

최대 부분 배열 문제는 배열에서 합이 최대가 되는 연속적인 부분 배열을 찾는 문제.

분할 정복 접근법:

1. 분할: 배열을 중간에서 두 부분으로 나눈다.
2. 정복: 왼쪽 부분 배열의 최대 부분 배열과 오른쪽 부분 배열의 최대 부분 배열을 재귀적으로 찾는다.
3. 결합: 왼쪽 부분의 최대값, 오른쪽 부분의 최대값, 그리고 중간을 가로지르는 부분의 최대값 중에서 가장 큰 값을 선택한다.

Python 구현:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

def max_subarray(arr, low=0, high=None):
    if high is None:
        high = len(arr) - 1
    
    # 베이스 케이스: 원소가 하나뿐인 경우
    if low == high:
        return arr[low]
    
    # 배열을 중간에서 분할
    mid = (low + high) // 2
    
    # 왼쪽 부분의 최대 부분 배열 합 찾기
    left_max = max_subarray(arr, low, mid)
    
    # 오른쪽 부분의 최대 부분 배열 합 찾기
    right_max = max_subarray(arr, mid + 1, high)
    
    # 중간을 가로지르는 최대 부분 배열 합 찾기
    cross_max = max_crossing_subarray(arr, low, mid, high)
    
    # 세 가지 경우 중 최대값 반환
    return max(left_max, right_max, cross_max)

def max_crossing_subarray(arr, low, mid, high):
    # 중간에서 왼쪽으로의 최대 합 찾기
    left_sum = float('-inf')
    sum = 0
    for i in range(mid, low - 1, -1):
        sum += arr[i]
        left_sum = max(left_sum, sum)
    
    # 중간에서 오른쪽으로의 최대 합 찾기
    right_sum = float('-inf')
    sum = 0
    for i in range(mid + 1, high + 1):
        sum += arr[i]
        right_sum = max(right_sum, sum)
    
    # 왼쪽과 오른쪽 합 결합
    return left_sum + right_sum

시간 복잡도: O(n log n)

Kadane의 알고리즘을 사용하면 이 문제를 O(n) 시간에 해결할 수 있지만, 분할 정복 접근법은 문제에 대한 다른 시각과 이해를 제공한다.

행렬 곱셈(Matrix Multiplication)

스트라센 알고리즘(Strassen’s Algorithm)은, n×n 행렬의 표준 곱셈보다 더 효율적인 분할 정복 방식의 행렬 곱셈 알고리즘이다.

알고리즘 개요:

1. 분할: 각 n×n 행렬을 4개의 n/2 × n/2 부분 행렬로 나눈다.
2. 정복: 7개의 특별한 곱셈(표준 방식은 8개 필요)을 통해 부분 행렬 곱을 계산한다.
3. 결합: 이 곱셈 결과를 조합하여 최종 결과 행렬을 생성한다.

시간 복잡도:

• 표준 행렬 곱셈: O(n³)
• 스트라센 알고리즘: O(n^log_2(7)) ≈ O(n^2.81)

이 알고리즘은 이론적으로 큰 행렬에 대해 더 효율적이지만, 실제로는 상수 요소와 구현 복잡성으로 인해 중간 크기 이상의 행렬에서만 이점이 있다.

분할 정복의 실제 응용 사례

1. 데이터베이스 시스템에서의 응용

   1. 인덱싱 및 검색:
      • B-트리와 B+트리는 분할 정복의 원리를 활용한 데이터베이스 인덱싱 구조.
      • 대용량 데이터에서의 효율적인 범위 검색에 활용된다.
   2. 쿼리 최적화:
      • 복잡한 SQL 쿼리를 더 작고 효율적인 하위 쿼리로 분해하는 최적화 기법에 분할 정복 원리가 적용된다.

2. 분산 컴퓨팅에서의 분할 정복

   1. 맵리듀스(MapReduce) 패러다임:
      • 구글에서 개발한 대규모 데이터 처리 프레임워크로, 분할 정복의 원리를 분산 환경에 적용한다.
      • Map 단계에서는 데이터를 작은 청크로 분할하여 독립적으로 처리한다.
      • Reduce 단계에서는 Map의 결과들을 결합하여 최종 결과를 생성한다.
      • Hadoop, Spark 등의 빅데이터 프레임워크가 이 패러다임을 구현한다.
   2. 분산 정렬:
      • TeraSort는 대용량 데이터를 분산 환경에서 정렬하는 알고리즘으로, 분할 정복 원리를 활용한다.
      • 데이터를 여러 노드에 분산시키고, 각 노드에서 독립적으로 정렬한 후, 최종적으로 병합한다.

3. 컴퓨터 그래픽스에서의 응용

   1. 레이 트레이싱(Ray Tracing):
      • 3D 렌더링 기술인 레이 트레이싱은 공간을 계층적으로 분할하여 광선-객체 교차 계산을 최적화한다.
      • 이를 위해 BSP 트리(Binary Space Partitioning Tree), 옥트리(Octree) 등의 공간 분할 자료구조를 사용한다.
   2. 이미지 압축:
      • 쿼드트리(Quadtree)를 사용한 이미지 압축은 이미지를 재귀적으로 4개의 사분면으로 분할하여 유사한 영역을 효율적으로 인코딩한다.
      • JPEG 2000과 같은 웨이블릿 기반 압축 알고리즘도 분할 정복 원리를 활용한다.

4. 머신러닝에서의 분할 정복

   1. 결정 트리(Decision Tree):
      • 결정 트리 학습 알고리즘은 데이터셋을 특성에 따라 재귀적으로 분할하여 분류 또는 회귀 모델을 구축한다.
      • ID3, C4.5, CART 등의 알고리즘이 이러한 접근법을 사용한다.
   2. 군집화(Clustering):
      • 계층적 군집화 알고리즘은 분할 정복 방식으로 데이터 포인트들을 그룹화한다.
      • 상향식(Bottom-up) 접근법에서는 각 포인트를 개별 클러스터로 시작하여 점진적으로 병합한다.
      • 하향식(Top-down) 접근법에서는 전체 데이터셋에서 시작하여 재귀적으로 분할한다.

7. 분할 정복의 변형과 확장

1. 분할과 정복(Split and Conquer)
   분할과 정복은 분할 정복의 변형으로, 문제를 여러 개의 독립적인 하위 문제로 나누지만, 원래 문제와 다른 형태의 하위 문제로 변환할 수 있다.
   예시: 선형 시간 선택 알고리즘(Linear-time Selection Algorithm):

   • 중앙값의 중앙값(Median of Medians) 알고리즘은 배열에서 k번째 작은 원소를 O(n) 시간에 찾을 수 있는 알고리즘이다:
     1. 배열을 5개 원소씩의 그룹으로 나눈다.
     2. 각 그룹에서 중앙값을 찾는다(삽입 정렬 등의 간단한 방법 사용).
     3. 이 중앙값들의 중앙값(피벗)을 재귀적으로 찾는다.
     4. 피벗을 기준으로 배열을 분할한다.
     5. 분할된 부분 중 하나를 선택하여 재귀적으로 탐색한다.
   • 이 알고리즘은 최악의 경우에도 O(n) 시간 복잡도를 보장한다.

2. 동적 프로그래밍과의 결합
   분할 정복과 동적 프로그래밍은 모두 문제를 더 작은 하위 문제로 나누지만, 하위 문제의 중복 여부에 따라 다른 접근법을 취한다:

   • 분할 정복: 일반적으로 중복되지 않는 하위 문제들을 해결
   • 동적 프로그래밍: 중복되는 하위 문제들의 해결책을 저장하고 재사용
     그러나 이 두 패러다임은 종종 결합될 수 있다.
     예를 들어:
   • 예시: 최적 이진 검색 트리(Optimal Binary Search Tree)
     • 주어진 검색 키와 각 키의 검색 빈도에 대해 평균 검색 시간을 최소화하는 이진 검색 트리를 구성하는 문제:
       1. 문제를 하위 문제로 분할: 서브트리를 구성하는 문제
       2. 중복되는 하위 문제 해결책을 테이블에 저장
       3. 최적 해를 상향식으로 구성
     • 이는 분할 정복의 재귀적 구조와 동적 프로그래밍의 메모이제이션을 결합한 접근법이다.

3. 확률적 분할 정복
   랜덤화를 분할 정복과 결합하여 평균적으로 더 효율적인 알고리즘을 만들 수 있다.

   • 예시: 랜덤화된 퀵 정렬(Randomized Quicksort)

     • 피벗을 무작위로 선택하는 퀵 정렬 변형이다:

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

     import random def randomized_quicksort(arr): if len(arr) <= 1: return arr # 랜덤 피벗 선택 pivot_idx = random.randint(0, len(arr) - 1) pivot = arr[pivot_idx] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return randomized_quicksort(left) + middle + randomized_quicksort(right)

     이 방식은 최악의 경우 O(n²) 시간 복잡도를 가질 수 있지만, 평균적으로 O(n log n)을 보장하며 실제로 매우 효율적이다.

4. 다차원 분할 정복
   분할 정복은 다차원 문제에도 효과적으로 적용될 수 있다.

   • 예시: k-d 트리(k-dimensional tree)
     • k-d 트리는 k차원 공간에서의 점들을 효율적으로 검색하기 위한 공간 분할 자료구조:
       1. 차원을 번갈아가며 공간을 분할합니다.
       2. 각 분할 단계에서 현재 차원의 중앙값을 기준으로 분할합니다.
       3. 이를 재귀적으로 반복하여 트리를 구성합니다.
     • k-d 트리는 근접 이웃 검색, 범위 검색 등 많은 공간 쿼리에 유용하다.

분할 정복의 미래 동향

1. 양자 컴퓨팅과 분할 정복
   양자 컴퓨팅은 분할 정복 알고리즘에 새로운 가능성을 제공한다:

   • 양자 검색 알고리즘: Grover의 알고리즘은 정렬되지 않은 데이터베이스에서 O(√n) 시간에 검색할 수 있다.
   • 양자 푸리에 변환: 고전적인 FFT를 더욱 효율적으로 구현할 수 있는 가능성을 제공한다.
   • 양자 병렬성: 양자 중첩을 통해 여러 하위 문제를 동시에 처리할 수 있는 잠재력이 있다.

2. 인공지능과의 결합
   분할 정복과 인공지능 기술의 통합은 흥미로운 발전을 보이고 있다:

   • 학습 기반 분할 전략: 머신러닝을 사용하여 최적의 분할 지점과 전략을 결정한다.
   • 신경망 가지치기: 대규모 신경망을 더 작은 하위 네트워크로 분할하여 효율적으로 학습 및 추론한다.
   • 자동 알고리즘 설계: AI가 문제에 최적화된 분할 정복 알고리즘을 자동으로 설계한다.

3. 분산 및 병렬 컴퓨팅의 발전
   분산 환경에서의 분할 정복 알고리즘 발전:

   • 엣지 컴퓨팅 최적화: 엣지 디바이스에서 효율적으로 실행할 수 있는 분할 정복 알고리즘
   • 이기종 컴퓨팅: CPU, GPU, TPU 등 다양한 프로세서에 최적화된 분할 정복 구현
   • 탄력적 확장성: 클라우드 환경에서 가용 자원에 따라 동적으로 조정되는 분할 정복 알고리즘

4. 새로운 응용 분야
   분할 정복이 활용될 수 있는 신흥 응용 분야:

   • 양자 역학 시뮬레이션: 복잡한 양자 시스템을 하위 시스템으로 분할하여 시뮬레이션
   • 생물정보학: 대규모 유전체 분석 및 단백질 구조 예측에서의 응용
   • 자율 시스템: 자율 주행 차량, 로봇 등에서의 복잡한 의사결정 문제 해결

참고 및 출처