힙 (Heap)

힙(Heap)은 완전 이진 트리(Complete Binary Tree) 기반의 특수한 트리 자료구조로, 특정한 순서 속성을 만족한다.
특히 우선순위 큐를 구현하는 데 효율적으로 사용되며, 다양한 알고리즘에서 핵심적인 역할을 한다.
힙은 최댓값이나 최솟값에 빠르게 접근해야 하는 상황에서 매우 유용한 자료구조이다.

힙은 효율적인 우선순위 접근과 관리를 제공하는 강력한 자료구조이다.
최댓값이나 최솟값에 빠르게 접근해야 하지만 다른 요소들의 전체 정렬은 필요하지 않을 때 특히 유용하다.
효율적인 삽입, 삭제, 최댓값/최솟값 접근 연산을 통해 다양한 알고리즘과 시스템에서 중요한 역할을 수행한다.

힙은 다른 자료구조와 함께 사용될 때 특히 강력하다. 예를 들어, 그래프 알고리즘에서 힙을 사용하면 효율성을 크게 높일 수 있다. 또한 다양한 문제에 대한 효율적인 해결책을 제공하며, 컴퓨터 과학의 기본적인 자료구조 중 하나로 자리 잡고 있다.

힙의 기본 개념

힙은 다음과 같은 속성을 가진 완전 이진 트리이다:

  1. 완전 이진 트리 구조: 모든 레벨이 완전히 채워져 있으며, 마지막 레벨은 왼쪽부터 차례로 채워진다.
  2. 힙 속성(Heap Property): 힙은 모든 노드가 다음 중 하나의 속성을 만족한다:
    • 최대 힙(Max Heap): 각 노드의 값은 그 자식 노드의 값보다 크거나 같다.
    • 최소 힙(Min Heap): 각 노드의 값은 그 자식 노드의 값보다 작거나 같다.
  3. 루트 노드: 최대 힙에서는 최댓값, 최소 힙에서는 최솟값이 루트 노드에 위치한다.

힙의 구조와 표현

힙은 일반적으로 배열을 사용하여 구현한다.
완전 이진 트리의 특성 때문에 배열로 효율적인 표현이 가능하다.
배열에서 인덱스 관계는 다음과 같다:

이러한 배열 표현은 포인터 없이도 트리 구조를 효율적으로 탐색할 수 있게 한다.

힙의 종류

최대 힙(Max Heap)

최대 힙에서는 각 노드의 값이 자식 노드의 값보다 크거나 같다.
따라서 루트 노드는 항상 힙 내의 최댓값을 가진다.

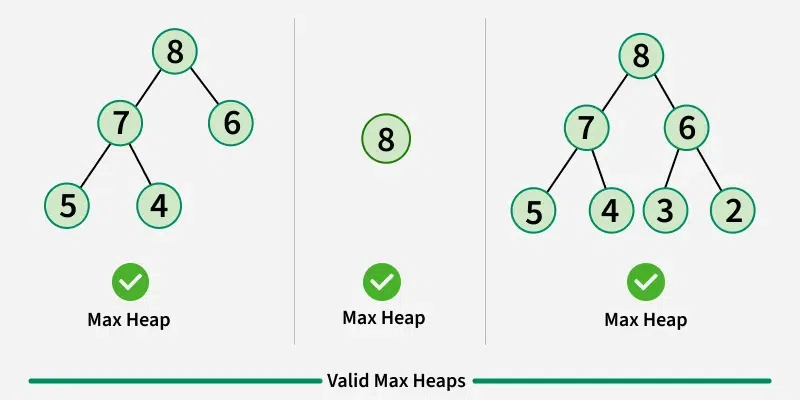
Max Heap
https://www.geeksforgeeks.org/introduction-to-heap/

예시:

1
2
3
4
5

      9
    /   \
   7     6
  / \   /
 5   4 3

2. 최소 힙(Min Heap)

최소 힙에서는 각 노드의 값이 자식 노드의 값보다 작거나 같다.
따라서 루트 노드는 항상 힙 내의 최솟값을 가진다.

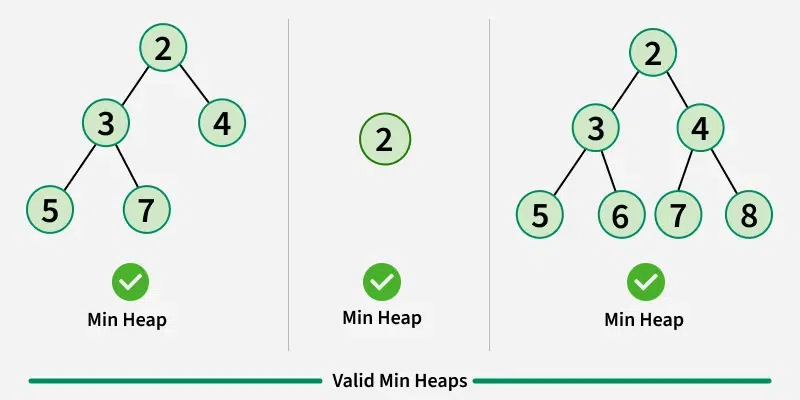
min Heap
https://www.geeksforgeeks.org/introduction-to-heap/

예시:

1
2
3
4
5

      1
    /   \
   3     2
  / \   /
 5   4 7

이항 힙(Binomial Heap)

이항 힙은 여러 개의 이항 트리로 구성된 힙이다.
두 힙을 병합하는 작업에 효율적인 특성을 가진다.

피보나치 힙(Fibonacci Heap)

피보나치 힙은 이항 힙의 확장으로, 특정 연산이 더 효율적이며 여러 트리의 모음으로 구성된다.

힙의 주요 연산

삽입(Insertion)

새 노드를 힙에 추가하는 과정이다.

  1. 새 노드를 힙의 마지막 위치(배열의 끝)에 추가한다.
  2. 새 노드와 부모 노드를 비교하여 힙 속성이 만족되지 않으면 교환한다.
  3. 힙 속성이 만족될 때까지 또는 루트에 도달할 때까지 2번 과정을 반복한다.

시간 복잡도: O(log n)

파이썬 구현 예시 (최대 힙):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

def insert_max_heap(heap, value):
    # 힙에 새 값 추가
    heap.append(value)
    # 새 값의 인덱스
    current = len(heap) - 1
    
    # 최대 힙 속성을 만족할 때까지 상향식으로 조정
    while current > 0:
        parent = (current - 1) // 2
        # 부모가 더 작으면 교환
        if heap[parent] < heap[current]:
            heap[parent], heap[current] = heap[current], heap[parent]
            current = parent
        else:
            break

최댓값/최솟값 추출(Extract Max/Min)

힙의 루트 노드(최댓값 또는 최솟값)를 제거하고 반환하는 과정이다.

  1. 루트 노드의 값을 저장한다.
  2. 마지막 노드를 루트 위치로 이동한다.
  3. 루트부터 시작하여 힙 속성이 만족될 때까지 노드를 자식 노드와 교환한다.
  4. 저장한 루트 값을 반환한다.

시간 복잡도: O(log n)

파이썬 구현 예시 (최대 힙):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

def extract_max(heap):
    if not heap:
        return None
    
    # 최댓값(루트) 저장
    max_value = heap[0]
    
    # 마지막 요소를 루트로 이동
    heap[0] = heap[-1]
    heap.pop()
    
    # 빈 힙이 되었다면 바로 반환
    if not heap:
        return max_value
    
    # 힙 속성 복원 (하향식 조정)
    current = 0
    while True:
        largest = current
        left = 2 * current + 1
        right = 2 * current + 2
        
        # 왼쪽 자식이 더 크면 교환 대상 변경
        if left < len(heap) and heap[left] > heap[largest]:
            largest = left
        
        # 오른쪽 자식이 더 크면 교환 대상 변경
        if right < len(heap) and heap[right] > heap[largest]:
            largest = right
        
        # 교환이 필요 없으면 반복 종료
        if largest == current:
            break
        
        # 교환
        heap[current], heap[largest] = heap[largest], heap[current]
        current = largest
    
    return max_value

힙 구성(Heapify)

배열을 힙 속성을 만족하는 형태로 재구성하는 연산이다.
이는 특정 노드부터 시작하여 그 하위 트리가 힙 속성을 만족하도록 조정하는 과정이.

파이썬 구현 예시 (최대 힙):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

def heapify(arr, n, i):
    """
    arr: 배열
    n: 배열의 크기
    i: 시작 인덱스
    """
    largest = i  # 현재 노드를 가장 큰 값으로 초기화
    left = 2 * i + 1
    right = 2 * i + 2
    
    # 왼쪽 자식이 현재 노드보다 크면 교체
    if left < n and arr[left] > arr[largest]:
        largest = left
    
    # 오른쪽 자식이 현재까지의 가장 큰 값보다 크면 교체
    if right < n and arr[right] > arr[largest]:
        largest = right
    
    # 가장 큰 값이 현재 노드가 아니라면 교환하고 재귀적으로 조정
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

힙 정렬(Heap Sort)

힙 속성을 활용하여 배열을 정렬하는 알고리즘이다.

  1. 주어진 배열을 힙으로 구성한다 (최대 힙 또는 최소 힙).
  2. 루트(최댓값 또는 최솟값)를 배열의 마지막 요소와 교환한다.
  3. 힙의 크기를 1 감소시키고, 새 루트에 대해 힙 속성을 복원한다.
  4. 힙의 크기가 1이 될 때까지 2-3 과정을 반복한다.

시간 복잡도: O(n log n)

파이썬 구현 예시:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

def heap_sort(arr):
    n = len(arr)
    
    # 최대 힙 구성 (비단말 노드부터 시작하여 루트까지)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)
    
    # 정렬 수행
    for i in range(n - 1, 0, -1):
        # 현재 루트(최댓값)를 마지막 요소와 교환
        arr[i], arr[0] = arr[0], arr[i]
        # 줄어든 힙에 대해 힙 속성 복원
        heapify(arr, i, 0)
    
    return arr

힙의 응용

  1. 우선순위 큐(Priority Queue)
    힙은 우선순위 큐를 구현하는 가장 효율적인 자료구조 중 하나이다.
    최소 힙은 가장 작은 우선순위의 요소를, 최대 힙은 가장 큰 우선순위의 요소를 O(1) 시간에 접근할 수 있게 한다.
    파이썬에서는 heapq 모듈을 통해 최소 힙 기반의 우선순위 큐를 쉽게 사용할 수 있다.

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

    import heapq

# 우선순위 큐 생성
priority_queue = []

# 요소 추가 (자동으로 힙 속성 유지)
heapq.heappush(priority_queue, 3)
heapq.heappush(priority_queue, 1)
heapq.heappush(priority_queue, 4)

# 최소값 추출
min_value = heapq.heappop(priority_queue)  # 1이 반환됨

  2. 다익스트라 알고리즘(Dijkstra’s Algorithm)
    최단 경로를 찾는 다익스트라 알고리즘에서 힙은 다음 방문할 노드를 효율적으로 선택하는 데 사용된다.

  3. 허프만 코딩(Huffman Coding)
    데이터 압축 알고리즘인 허프만 코딩에서는 최소 힙을 사용하여 가장 빈도가 낮은 두 기호를 효율적으로 선택한다.

  4. 메디안 유지(Finding Median in Stream of Integers)
    데이터 스트림에서 중앙값(미디언)을 효율적으로 찾는 문제는 최대 힙과 최소 힙을 함께 사용하여 해결할 수 있다.

  5. 힙 정렬(Heap Sort)
    앞서 설명한 힙 정렬은 안정적인 O(n log n) 시간 복잡도를 가지는 정렬 알고리즘이다.

힙의 시간 복잡도 분석

연산시간 복잡도
삽입(Insert)O(log n)
최댓값/최솟값 접근(Get Max/Min)O(1)
최댓값/최솟값 추출(Extract Max/Min)O(log n)
힙 구성(Build Heap)O(n)
정렬(Heap Sort)O(n log n)

다양한 언어에서의 힙 구현

Java에서의 힙 구현

Java에서는 PriorityQueue 클래스가 힙을 기반으로 구현되어 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import java.util.PriorityQueue;

public class HeapExample {
    public static void main(String[] args) {
        // 최소 힙 (기본)
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        
        // 요소 추가
        minHeap.add(3);
        minHeap.add(1);
        minHeap.add(4);
        
        // 최소값 추출
        System.out.println(minHeap.poll());  // 1 출력
        
        // 최대 힙 (Comparator 사용)
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
        
        // 요소 추가
        maxHeap.add(3);
        maxHeap.add(1);
        maxHeap.add(4);
        
        // 최대값 추출
        System.out.println(maxHeap.poll());  // 4 출력
    }
}

파이썬에서의 힙 구현

파이썬은 heapq 모듈을 통해 최소 힙을 지원한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

import heapq

# 최소 힙 생성 (기본)
min_heap = []
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 4)

# 최소값 추출
print(heapq.heappop(min_heap))  # 1 출력

# 최대 힙 구현 (값에 -1을 곱하는 방식)
max_heap = []
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -4)

# 최대값 추출 (-1을 곱해 복원)
print(-heapq.heappop(max_heap))  # 4 출력

힙의 구현에서 주의할 점

  1. 인덱스 계산: 배열로 힙을 구현할 때 인덱스 계산에 주의해야 한다.
  2. 최대/최소 힙 선택: 문제의 요구사항에 따라 적절한 힙을 선택해야 한다.
  3. 힙 속성 유지: 삽입과 삭제 후 힙 속성이 유지되는지 확인해야 한다.
  4. 효율성: 힙 연산의 효율성을 위해 불필요한 연산을 최소화해야 한다.

힙의 확장과 변형

  1. 이중 힙(Double-Ended Heap)
    최솟값과 최댓값을 모두 O(1) 시간에 접근할 수 있도록 구현된 힙이다.
    흔히 ‘민맥스 힙(Min-Max Heap)‘이라고도 부른다.

  2. 섬유 힙(Leftist Heap)
    병합 연산이 효율적인 힙의 한 종류로, 균형이 한쪽으로 치우친 구조를 가진다.

  3. 스키우 힙(Skew Heap)
    섬유 힙과 유사하지만 구조가 더 간단하다.
    모든 연산 후 트리를 재구성한다.

  4. d-힙(d-Heap)
    각 노드가 2개가 아닌 d개의 자식을 가지는 힙이다.
    메모리 접근 패턴에 따라 더 효율적일 수 있다.

실제 응용 사례

  1. 운영체제에서의 스케줄링
    운영체제에서 우선순위가 높은 프로세스를 효율적으로 선택하기 위해 힙을 사용한다.

  2. 네트워크 라우팅
    최단 경로 알고리즘에서 다음 방문할 노드를 결정하는 데 힙을 사용한다.

  3. 데이터베이스 인덱싱
    일부 데이터베이스 시스템에서는 인덱스 구조에 힙과 유사한 자료구조를 활용한다.

  4. 이벤트 시뮬레이션
    이벤트 기반 시뮬레이션에서 다음 처리할 이벤트를 결정하기 위해 힙을 사용한다.

참고 및 출처