인접 행렬(Adjacency Matrix)

인접 행렬(Adjacency Matrix)

인접 행렬은 그래프를 표현하는 가장 기본적인 방법 중 하나로, 수학적 행렬을 사용하여 그래프의 정점들 간의 연결 관계를 나타낸다.
행렬의 각 원소는 두 정점 사이의 간선 존재 여부나 가중치를 표시한다.

인접 행렬은 그래프를 표현하는 직관적이고 효율적인 방법이다. 특히 간선의 존재 여부를 빠르게 확인해야 하거나, 간선이 많은 밀집 그래프를 다룰 때 유용하다. 또한, 행렬 연산을 통해 그래프의 다양한 속성을 분석할 수 있다는 장점이 있다.

하지만 정점이 많고 간선이 적은 희소 그래프에서는 메모리 사용량이 많아지는 단점이 있다. 이러한 경우에는 인접 리스트나 희소 행렬 표현과 같은 대안을 고려할 필요가 있다.

인접 행렬의 기본 개념

인접 행렬 A는 n×n 크기의 2차원 배열로, n은 그래프의 정점 수이다.

행렬의 각 원소 A[i][j]는 다음과 같이 정의된다:

• 무가중치 그래프의 경우
  • A[i][j] = 1: 정점 i에서 정점 j로 가는 간선이 존재
  • A[i][j] = 0: 정점 i에서 정점 j로 가는 간선이 없음
• 가중치 그래프의 경우
  • A[i][j] = w: 정점 i에서 정점 j로 가는 간선의 가중치가 w
  • A[i][j] = ∞ (또는 매우 큰 값): 정점 i에서 정점 j로 가는 간선이 없음
  • 때로는 A[i][j] = 0을 간선이 없음을 나타내는 데 사용하기도 한다.

인접 행렬의 특성

무방향 그래프에서의 인접 행렬

무방향 그래프에서는 i에서 j로 가는 간선이 있다면, j에서 i로 가는 간선도 있다.
따라서:

• A[i][j] = A[j][i]가 항상 성립한다.
• 인접 행렬이 대칭 행렬(symmetric matrix)이 된다.
• 자기 자신으로의 간선(자기 루프)이 없는 경우, 대각선 원소들은 모두 0이다.

Adjacency Matrix for Undirected and Unweighted graph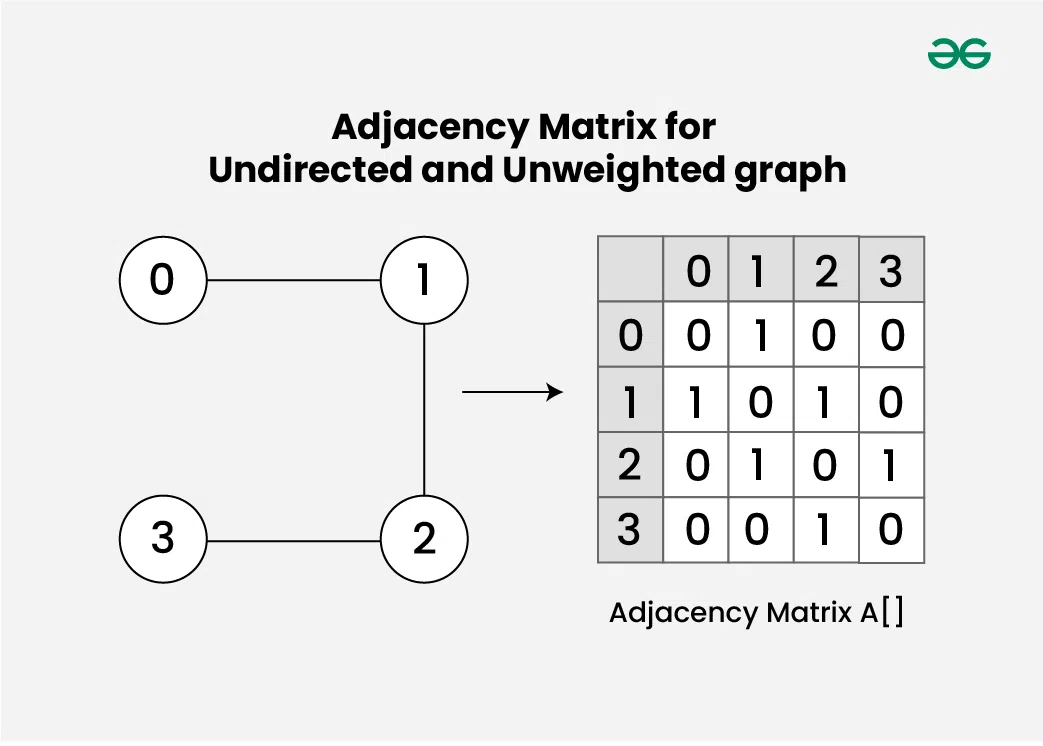

Adjacency Matrix for Undirected and Weighted graph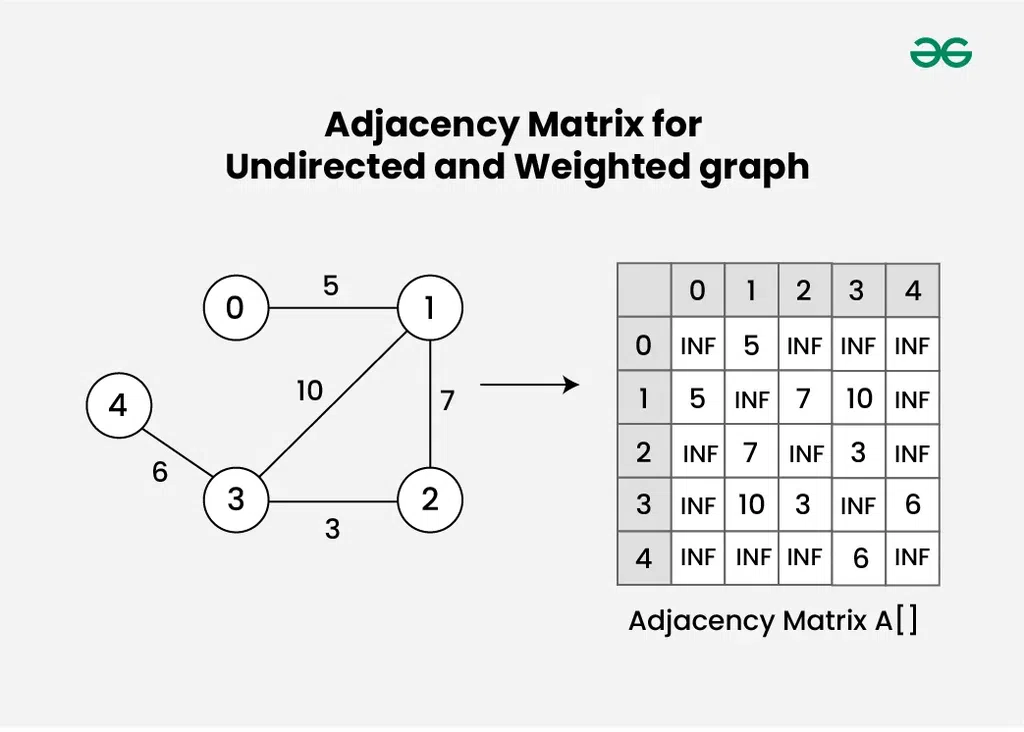

방향 그래프에서의 인접 행렬

방향 그래프에서는 i에서 j로 가는 간선이 있더라도, j에서 i로 가는 간선이 없을 수 있다:

• A[i][j]와 A[j][i]가 다를 수 있다.
• 인접 행렬이 비대칭 행렬일 수 있다.

Adjacency Matrix for Directed and Unweighted graph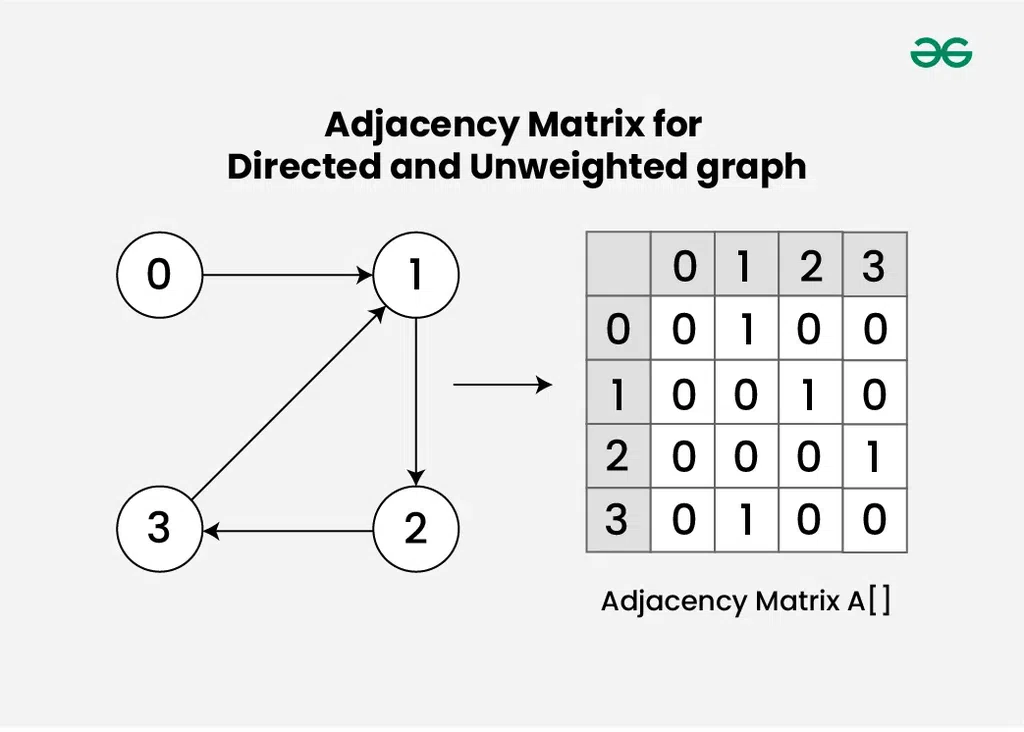

Adjacency Matrix for Directed and Weighted graph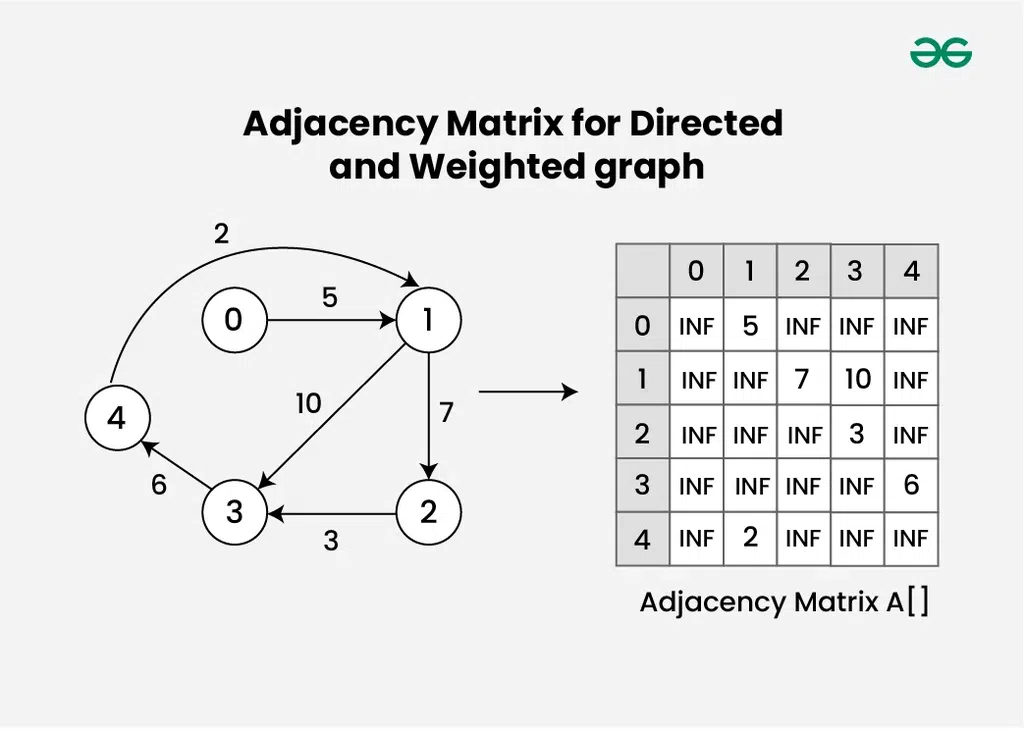

인접 행렬의 장단점

인접 행렬은 간선 정보를 빠르게 조회해야 하는 경우 적합하지만, 간선이 적은 희소 그래프(Sparse Graph)에서는 비효율적이다.
간선 개수가 많고 밀집된 그래프(Dense Graph)에서 더 유용하게 사용된다.

장점

1. 간단한 구현: 2차원 배열만 있으면 쉽게 구현할 수 있다.
2. 간선 확인의 효율성: 두 정점 사이의 간선 존재 여부를 O(1) 시간에 확인할 수 있다.
3. 간선 추가/제거의 효율성: 간선 추가 및 제거가 O(1) 시간에 가능하다.
4. 밀집 그래프(Dense Graph)에서의 효율성: 간선이 많은 그래프에서는 메모리 효율이 좋을 수 있다.
5. 행렬 연산 활용: 그래프 이론의 많은 부분을 행렬 연산으로 처리할 수 있다.

단점

1. 공간 복잡도: O(V²) 공간을 차지하므로, 정점이 많은 그래프에서는 메모리 사용량이 많다.
2. 희소 그래프(Sparse Graph)에서의 비효율성: 간선이 적은 그래프에서는 많은 메모리가 낭비된다.
3. 모든 간선 순회: 특정 정점의 모든 인접 정점을 찾기 위해 O(V) 시간이 필요하다. 인접 리스트를 사용하면 인접한 정점의 수에 비례하는 시간만 필요하다.

인접 행렬의 수학적 특성

1. 행렬의 거듭제곱
   그래프의 인접 행렬 A에 대해, A^k[i][j]는 정점 i에서 정점 j로 가는 길이가 정확히 k인 경로의 수를 나타낸다.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   import numpy as np def count_paths_of_length_k(adj_matrix, k): """ 길이가 정확히 k인 경로의 수를 계산합니다. Args: adj_matrix (list of list): 인접 행렬 k (int): 경로의 길이 Returns: numpy.ndarray: 결과 행렬 (A^k) """ A = np.array(adj_matrix) return np.linalg.matrix_power(A, k)

   이 속성은 그래프 분석에서 매우 유용하게 활용된다.
   예를 들어, 소셜 네트워크에서 A^2[i][j]는 사용자 i와 사용자 j가 공통으로 아는 친구의 수를 나타낸다.

2. 인접 행렬과 그래프 특성

   1. 연결 그래프 판별: A + A² + A³ + … + A^(n-1)의 모든 원소가 0이 아니면, 그래프는 연결 그래프이다.
   2. 정점의 중심성(Centrality): 인접 행렬의 고유벡터(eigenvector)가 정점의 중심성을 나타낼 수 있다. 이는 PageRank 알고리즘의 기본 원리이다.
   3. 그래프 정규화(Regularization): 정규화된 인접 행렬 D^(-1/2)AD^(-1/2) (여기서 D는 대각 행렬로, D[i][i]는 정점 i의 차수)는 그래프 신호 처리와 기계 학습에서 중요하게 사용된다.

인접 행렬의 구조

무방향 그래프 (Undirected Graph)의 인접 행렬

무방향 그래프에서는 간선이 양방향이므로, 대칭 행렬(Symmetric Matrix) 형태를 가진다.

예제 그래프

1
2
3

  A - B
  |   |
  C - D

인접 행렬 표현

방향 그래프 (Directed Graph)의 인접 행렬

방향 그래프는 간선이 **한쪽 방향으로만 연결되므로, 비대칭 행렬(Asymmetric Matrix)이 될 수 있다.

예제 그래프

1
2
3

  A → B
  ↓   
  C → D

인접 행렬 표현

가중치 그래프 (Weighted Graph)의 인접 행렬

가중치 그래프에서는 0과 1 대신, 간선의 가중치(Weight)를 저장한다.

예제 그래프

1
2
3
4
5

  A --(4)--> B
  |         |
 (2)       (3)
  |         |
  C --(1)--> D

인접 행렬 표현

Python을 이용한 인접 행렬 구현 예시

기본 인접 행렬 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

# 그래프의 노드 수
V = 4

# 4 x 4 크기의 인접 행렬 생성 (초기값 0)
adj_matrix = [[0] * V for _ in range(V)]

# 간선 추가 (A=0, B=1, C=2, D=3)
edges = [(0, 1), (0, 2), (2, 3)]

# 간선 정보를 인접 행렬에 반영
for u, v in edges:
    adj_matrix[u][v] = 1  # 방향 그래프 (무방향 그래프라면 adj_matrix[v][u] = 1도 추가)

# 인접 행렬 출력
for row in adj_matrix:
    print(row)

출력 결과

1
2
3
4

[0, 1, 1, 0]
[0, 0, 0, 0]
[0, 0, 0, 1]
[0, 0, 0, 0]

가중치 그래프 인접 행렬 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

V = 4
INF = float('inf')  # 간선이 없는 경우를 무한대(INF)로 표시

# 4 x 4 크기의 가중치 인접 행렬 생성 (초기값 INF)
adj_matrix = [[INF] * V for _ in range(V)]

# 자기 자신으로 가는 간선은 0으로 설정
for i in range(V):
    adj_matrix[i][i] = 0

# 간선 추가 (A=0, B=1, C=2, D=3) - (출발, 도착, 가중치)
edges = [(0, 1, 4), (0, 2, 2), (2, 3, 1), (1, 3, 3)]

for u, v, weight in edges:
    adj_matrix[u][v] = weight  # 방향 그래프

# 인접 행렬 출력
for row in adj_matrix:
    print(row)

출력 결과

1
2
3
4

[0, 4, 2, INF]
[INF, 0, INF, 3]
[INF, INF, 0, 1]
[INF, INF, INF, 0]

인접 행렬 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

class Graph:
    def __init__(self, num_vertices, directed=False):
        """
        그래프의 정점 수를 받아 인접 행렬을 초기화합니다.
        
        Args:
            num_vertices (int): 정점의 개수
            directed (bool): 방향 그래프 여부 (기본값: False)
        """
        self.num_vertices = num_vertices
        self.directed = directed
        
        # 인접 행렬 초기화 (모든 원소를 0으로 설정)
        self.adj_matrix = [[0 for _ in range(num_vertices)] for _ in range(num_vertices)]
    
    def add_edge(self, v1, v2, weight=1):
        """
        그래프에 간선을 추가합니다.
        
        Args:
            v1 (int): 시작 정점
            v2 (int): 도착 정점
            weight (int/float): 간선의 가중치 (기본값: 1)
        """
        if v1 >= self.num_vertices or v2 >= self.num_vertices or v1 < 0 or v2 < 0:
            print("유효하지 않은 정점입니다.")
            return
        
        self.adj_matrix[v1][v2] = weight
        
        # 무방향 그래프인 경우 대칭적으로 간선 추가
        if not self.directed:
            self.adj_matrix[v2][v1] = weight
    
    def remove_edge(self, v1, v2):
        """
        그래프에서 간선을 제거합니다.
        
        Args:
            v1 (int): 시작 정점
            v2 (int): 도착 정점
        """
        if v1 >= self.num_vertices or v2 >= self.num_vertices or v1 < 0 or v2 < 0:
            print("유효하지 않은 정점입니다.")
            return
        
        self.adj_matrix[v1][v2] = 0
        
        # 무방향 그래프인 경우 대칭적으로 간선 제거
        if not self.directed:
            self.adj_matrix[v2][v1] = 0
    
    def print_graph(self):
        """
        인접 행렬을 출력합니다.
        """
        for i in range(self.num_vertices):
            for j in range(self.num_vertices):
                print(self.adj_matrix[i][j], end=" ")
            print()
    
    def get_neighbors(self, vertex):
        """
        특정 정점에 인접한 정점들을 반환합니다.
        
        Args:
            vertex (int): 정점
            
        Returns:
            list: 인접한 정점들의 리스트
        """
        if vertex >= self.num_vertices or vertex < 0:
            print("유효하지 않은 정점입니다.")
            return []
            
        neighbors = []
        for i in range(self.num_vertices):
            if self.adj_matrix[vertex][i] != 0:
                neighbors.append(i)
        
        return neighbors

인접 행렬을 이용한 그래프 연산

인접한 정점 찾기

1
2
3
4
5
6
7

# vertex의 모든 인접 정점 찾기
def get_neighbors(adj_matrix, vertex):
    neighbors = []
    for i in range(len(adj_matrix)):
        if adj_matrix[vertex][i] != 0:
            neighbors.append(i)
    return neighbors

간선의 존재 여부 확인

1
2
3

# v1에서 v2로 가는 간선이 있는지 확인
def is_edge(adj_matrix, v1, v2):
    return adj_matrix[v1][v2] != 0

정점의 차수(degree) 계산

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 무방향 그래프에서 vertex의 차수 계산
def get_degree(adj_matrix, vertex):
    degree = 0
    for i in range(len(adj_matrix)):
        if adj_matrix[vertex][i] != 0:
            degree += 1
    return degree

# 방향 그래프에서 정점의 진입 차수(in-degree) 계산
def get_in_degree(adj_matrix, vertex):
    in_degree = 0
    for i in range(len(adj_matrix)):
        if adj_matrix[i][vertex] != 0:
            in_degree += 1
    return in_degree

# 방향 그래프에서 정점의 진출 차수(out-degree) 계산
def get_out_degree(adj_matrix, vertex):
    out_degree = 0
    for i in range(len(adj_matrix)):
        if adj_matrix[vertex][i] != 0:
            out_degree += 1
    return out_degree

인접 행렬을 이용한 그래프 알고리즘

1. 깊이 우선 탐색(DFS)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

   def dfs_adjacency_matrix(adj_matrix, start_vertex): """ 인접 행렬로 표현된 그래프에서 DFS 수행 Args: adj_matrix (list of list): 인접 행렬 start_vertex (int): 시작 정점 Returns: list: 방문한 정점들의 순서 """ n = len(adj_matrix) visited = [False] * n result = [] def dfs_recursive(vertex): # 현재 정점을 방문 처리 visited[vertex] = True result.append(vertex) # 인접한 정점들을 방문 for i in range(n): if adj_matrix[vertex][i] != 0 and not visited[i]: dfs_recursive(i) dfs_recursive(start_vertex) return result

2. 너비 우선 탐색(BFS)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

   from collections import deque def bfs_adjacency_matrix(adj_matrix, start_vertex): """ 인접 행렬로 표현된 그래프에서 BFS 수행 Args: adj_matrix (list of list): 인접 행렬 start_vertex (int): 시작 정점 Returns: list: 방문한 정점들의 순서 """ n = len(adj_matrix) visited = [False] * n result = [] # 시작 정점을 큐에 넣고 방문 처리 queue = deque([start_vertex]) visited[start_vertex] = True while queue: # 큐에서 정점을 하나 꺼내서 결과에 추가 vertex = queue.popleft() result.append(vertex) # 인접한 정점들을 큐에 추가 for i in range(n): if adj_matrix[vertex][i] != 0 and not visited[i]: visited[i] = True queue.append(i) return result

3. 다익스트라(Dijkstra) 알고리즘

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

   import heapq def dijkstra_adjacency_matrix(adj_matrix, start_vertex): """ 인접 행렬로 표현된 그래프에서 다익스트라 알고리즘 수행 Args: adj_matrix (list of list): 인접 행렬 start_vertex (int): 시작 정점 Returns: list: 시작 정점에서 각 정점까지의 최단 거리 """ n = len(adj_matrix) distances = [float('inf')] * n # 최단 거리를 저장할 배열 distances[start_vertex] = 0 # 시작 정점의 거리는 0 # (현재까지의 거리, 정점) 튜플을 원소로 하는 최소 힙 priority_queue = [(0, start_vertex)] while priority_queue: # 가장 거리가 짧은 정점 선택 current_distance, current_vertex = heapq.heappop(priority_queue) # 이미 처리된 정점이면 스킵 if current_distance > distances[current_vertex]: continue # 인접한 정점들의 거리 갱신 for neighbor in range(n): # 간선이 존재하는 경우에만 처리 if adj_matrix[current_vertex][neighbor] != 0: distance = current_distance + adj_matrix[current_vertex][neighbor] # 더 짧은 경로를 발견한 경우 갱신 if distance < distances[neighbor]: distances[neighbor] = distance heapq.heappush(priority_queue, (distance, neighbor)) return distances

인접 행렬의 실제 활용 사례

1. 소셜 네트워크 분석
   페이스북, 트위터와 같은 소셜 미디어 플랫폼에서는 사용자 간의 관계를 인접 행렬로 표현할 수 있다:

   • A[i][j] = 1: 사용자 i가 사용자 j를 팔로우하거나 친구인 경우
   • A[i][j] = 0: 그렇지 않은 경우
     이를 통해 다음과 같은 분석이 가능하다:
   • 공통 친구 수 계산 (A²[i][j])
   • 영향력 있는 사용자 식별 (중심성 분석)
   • 커뮤니티 감지 (군집 분석)

2. 웹 그래프와 검색 엔진
   웹 페이지들을 정점으로, 하이퍼링크를 간선으로 표현하는 웹 그래프에서:

   • PageRank 알고리즘은 인접 행렬의 고유벡터를 계산하여 페이지의 중요도를 결정한다.
   • HITS(Hyperlink-Induced Topic Search) 알고리즘은 인접 행렬과 그 전치 행렬을 사용하여 허브(hub)와 권위(authority) 페이지를 식별한다.

3. 네트워크 라우팅
   컴퓨터 네트워크에서 라우터 간의 연결을 나타내는 인접 행렬:

   • 플로이드-워셜(Floyd-Warshall) 알고리즘을 사용하여 모든 라우터 쌍 간의 최단 경로를 계산한다.
   • 스패닝 트리 프로토콜(STP)은 최소 신장 트리를 구성하여 루프를 방지한다.

4. 생물학적 네트워크
   단백질 상호작용 네트워크나 유전자 조절 네트워크:

   • 인접 행렬을 통해 생물학적 경로와 기능적 모듈을 식별한다.
   • 네트워크 모티프(motif) 분석을 통해 반복적으로 나타나는 패턴을 찾는다.

인접 행렬 최적화 기법

1. 희소 행렬(Sparse Matrix) 표현
   정점은 많지만 간선이 적은 희소 그래프의 경우, 희소 행렬 자료구조를 사용하여 메모리 사용량을 줄일 수 있다:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

   from scipy.sparse import csr_matrix # 희소 인접 행렬 생성 def create_sparse_adjacency_matrix(edges, num_vertices): """ 희소 인접 행렬을 생성합니다. Args: edges (list of tuple): (시작 정점, 끝 정점, 가중치) 형태의 간선 목록 num_vertices (int): 정점의 수 Returns: scipy.sparse.csr_matrix: 희소 인접 행렬 """ row = [edge[0] for edge in edges] col = [edge[1] for edge in edges] data = [edge[2] for edge in edges] return csr_matrix((data, (row, col)), shape=(num_vertices, num_vertices))

2. 블록 행렬(Block Matrix) 표현
   큰 그래프를 여러 개의 작은 블록으로 나누어 처리할 수 있다.
   이는 분산 시스템에서 유용하다:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

   def create_block_adjacency_matrix(adj_matrix, block_size): """ 인접 행렬을 블록 단위로 나눕니다. Args: adj_matrix (list of list): 인접 행렬 block_size (int): 블록의 크기 Returns: list of list of list: 블록 인접 행렬 """ n = len(adj_matrix) num_blocks = (n + block_size - 1) // block_size block_matrix = [[[] for _ in range(num_blocks)] for _ in range(num_blocks)] for i in range(num_blocks): for j in range(num_blocks): # 블록의 범위 계산 row_start = i * block_size row_end = min((i + 1) * block_size, n) col_start = j * block_size col_end = min((j + 1) * block_size, n) # 블록 생성 block = [] for r in range(row_start, row_end): row = [] for c in range(col_start, col_end): row.append(adj_matrix[r][c]) block.append(row) block_matrix[i][j] = block return block_matrix

참고 및 출처