그래프 (Graph)

그래프는 컴퓨터 과학에서 가장 유연하고 강력한 자료구조 중 하나이다.
다양한 관계를 표현할 수 있어 현실 세계의 복잡한 문제를 모델링하는 데 매우 유용하다.

그래프는 다양한 문제를 해결하는 데 사용되는 강력한 자료구조이다.
인접 행렬, 인접 리스트, 간선 리스트 등 다양한 방법으로 표현할 수 있으며, DFS, BFS 등의 탐색 알고리즘부터 다익스트라, 벨만-포드 등의 최단 경로 알고리즘, 크루스칼, 프림 등의 최소 신장 트리 알고리즘까지 다양한 알고리즘이 그래프에 적용된다.

현실 세계의 많은 문제들을 그래프로 모델링할 수 있기 때문에, 그래프 이론은 컴퓨터 과학에서 매우 중요한 분야이다.
특히 소셜 네트워크, 내비게이션 시스템, 웹 페이지 랭킹 등 현대 기술의 핵심 부분에 그래프 알고리즘이 적용되고 있다.

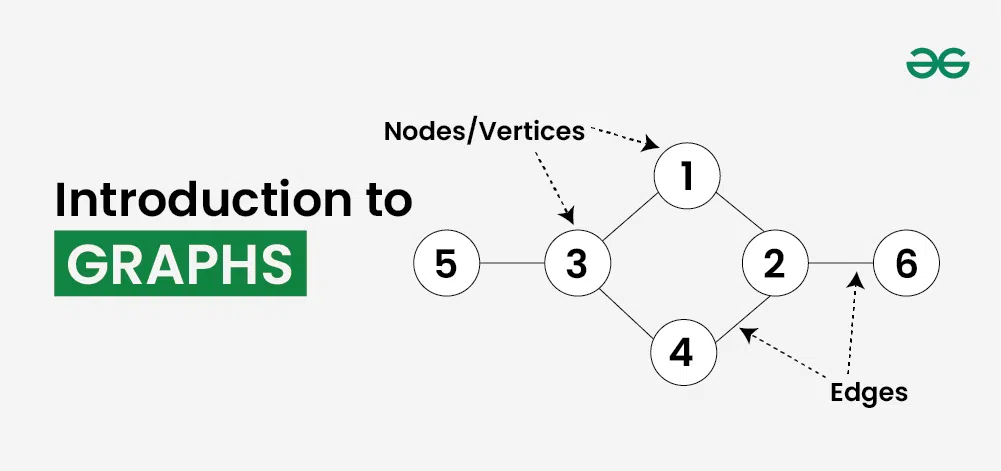
Graph Data Structure — https://www.geeksforgeeks.org/introduction-to-graphs-data-structure-and-algorithm-tutorials/

그래프의 기본 개념

그래프 G는 정점(또는 노드) 집합 V와 간선(또는 엣지) 집합 E로 구성되며, G = (V, E)로 표기한다.

정점(Vertex): 그래프의 기본 요소로, 객체나 위치를 나타낸다.
간선(Edge): 정점들 간의 관계나 연결을 나타낸다.

예를 들어, 소셜 네트워크에서 사람들은 정점이 되고, 친구 관계는 간선이 된다.

그래프의 종류

방향성에 따른 분류

무방향 그래프(Undirected Graph): 간선에 방향이 없어 양방향으로 이동 가능하다.
- 수학적으로 간선 (u, v)와 (v, u)는 동일하다.
- 예: 페이스북 친구 관계
방향 그래프(Directed Graph 또는 Digraph): 간선에 방향이 있어 한쪽 방향으로만 이동 가능하다.
- 간선이 화살표로 표시되며, (u, v)는 u에서 v로의 방향을 의미한다.
- 예: 트위터 팔로우 관계, 도로의 일방통행

가중치에 따른 분류

가중치 그래프(Weighted Graph): 간선에 가중치(비용, 거리, 시간 등)가 할당된다.
- 예: 도시 간 거리를 나타내는 지도
비가중치 그래프(Unweighted Graph): 모든 간선의 가중치가 동일하거나 무시된다.

연결성에 따른 분류

연결 그래프(Connected Graph): 모든 정점 쌍 사이에 경로가 존재한다.
비연결 그래프(Disconnected Graph): 적어도 하나의 정점 쌍 사이에 경로가 없다.

순환성에 따른 분류

순환 그래프(Cyclic Graph): 적어도 하나의 순환(cycle)이 존재한다.
비순환 그래프(Acyclic Graph): 순환이 없는 그래프이다.
DAG(Directed Acyclic Graph): 방향이 있고 순환이 없는 그래프이다.
- 예: 작업 스케줄링, 의존성 관리

특수한 그래프

완전 그래프(Complete Graph): 모든 정점 쌍이 간선으로 연결된 그래프이다.
이분 그래프(Bipartite Graph): 정점을 두 그룹으로 나눌 수 있고, 같은 그룹 내의 정점 간에는 간선이 없는 그래프이다.
트리(Tree): 순환이 없는 연결 그래프이다.

그래프의 표현 방법

인접 행렬(Adjacency Matrix)

n×n 행렬(n은 정점의 수)을 사용하여 그래프를 표현한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
# 인접 행렬을 이용한 그래프 표현 예시
class Graph:
    def __init__(self, vertices):
        self.V = vertices  # 정점의 수
        self.graph = [[0 for _ in range(vertices)] for _ in range(vertices)]  # 인접 행렬 초기화
        
    def add_edge(self, u, v, weight=1):
        self.graph[u][v] = weight  # u에서 v로 가는 간선 추가
        # 무방향 그래프의 경우 아래 코드도 추가
        # self.graph[v][u] = weight

장점:

두 정점 간의 간선 존재 여부를 O(1) 시간에 확인 가능
구현이 간단함

단점:

O(V²) 공간 복잡도로, 희소 그래프(sparse graph)에서 메모리 낭비가 심함
모든 간선을 순회하는 데 O(V²) 시간이 필요함

인접 리스트(Adjacency List)

각 정점마다 인접한 정점들의 리스트를 유지한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
# 인접 리스트를 이용한 그래프 표현 예시
class Graph:
    def __init__(self, vertices):
        self.V = vertices  # 정점의 수
        self.graph = [[] for _ in range(vertices)]  # 인접 리스트 초기화
        
    def add_edge(self, u, v, weight=1):
        self.graph[u].append((v, weight))  # u에서 v로 가는 간선 추가
        # 무방향 그래프의 경우 아래 코드도 추가
        # self.graph[v].append((u, weight))

장점:

O(V+E) 공간 복잡도로, 희소 그래프에서 효율적
모든 간선을 순회하는 데 O(V+E) 시간이 필요함

단점:

두 정점 간의 간선 존재 여부를 확인하는 데 O(degree(V)) 시간이 필요함

간선 리스트(Edge List)

모든 간선을 리스트로 저장한다.

1
2
3
4
5
6
7
8
# 간선 리스트를 이용한 그래프 표현 예시
class Graph:
    def __init__(self, vertices):
        self.V = vertices  # 정점의 수
        self.edges = []  # 간선 리스트 초기화
        
    def add_edge(self, u, v, weight=1):
        self.edges.append((u, v, weight))  # u에서 v로 가는 간선 추가

장점:

구현이 매우 간단함
크루스칼 알고리즘과 같이 간선을 정렬해야 하는 알고리즘에 적합함

단점:

두 정점 간의 간선 존재 여부를 확인하는 데 O(E) 시간이 필요함
특정 정점에 인접한 모든 정점을 찾는 데 비효율적임

그래프 탐색 알고리즘

깊이 우선 탐색(DFS, Depth-First Search)
스택 또는 재귀를 사용하여 가능한 한 깊이 탐색한 후 백트래킹한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
# DFS 구현 예시 (인접 리스트 사용)
def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()

    visited.add(start)
    print(start, end=' ')  # 방문한 정점 출력

    for neighbor, _ in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

시간 복잡도: O(V+E)

너비 우선 탐색(BFS, Breadth-First Search)
큐를 사용하여, 시작 정점으로부터 거리가 가까운 순서대로 탐색한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
# BFS 구현 예시 (인접 리스트 사용)
from collections import deque

def bfs(graph, start):
    visited = set([start])
    queue = deque([start])

    while queue:
        vertex = queue.popleft()
        print(vertex, end=' ')  # 방문한 정점 출력

        for neighbor, _ in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

시간 복잡도: O(V+E)

최단 경로 알고리즘

다익스트라 알고리즘(Dijkstra’s Algorithm)
음수 가중치가 없는 그래프에서 한 정점에서 다른 모든 정점까지의 최단 경로를 찾는다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 다익스트라 알고리즘 구현 예시 (인접 행렬 사용)
import heapq

def dijkstra(graph, start):
    n = len(graph)
    distances = [float('inf')] * n  # 시작 정점에서 각 정점까지의 거리
    distances[start] = 0
    priority_queue = [(0, start)]  # (거리, 정점) 튜플

    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        # 현재 거리가 이미 계산된 거리보다 크면 무시
        if current_distance > distances[current_vertex]:
            continue

        # 인접한 정점들을 확인
        for neighbor in range(n):
            if graph[current_vertex][neighbor] > 0:  # 간선이 존재하는 경우
                distance = current_distance + graph[current_vertex][neighbor]

                # 더 짧은 경로를 발견한 경우
                if distance < distances[neighbor]:
                    distances[neighbor] = distance
                    heapq.heappush(priority_queue, (distance, neighbor))

    return distances

시간 복잡도: O((V+E)log V) (최소 힙 사용 시)

벨만-포드 알고리즘(Bellman-Ford Algorithm)
음수 가중치가 있는 그래프에서도 최단 경로를 찾을 수 있다. 또한 음수 사이클을 감지할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
# 벨만-포드 알고리즘 구현 예시 (간선 리스트 사용)
def bellman_ford(graph, start):
    n = graph.V
    distances = [float('inf')] * n
    distances[start] = 0

    # 모든 정점에 대해 V-1번 반복
    for _ in range(n - 1):
        # 모든 간선에 대해 완화(relaxation) 수행
        for u, v, weight in graph.edges:
            if distances[u] != float('inf') and distances[u] + weight < distances[v]:
                distances[v] = distances[u] + weight

    # 음수 사이클 감지
    for u, v, weight in graph.edges:
        if distances[u] != float('inf') and distances[u] + weight < distances[v]:
            print("음수 사이클이 존재합니다.")
            return None

    return distances

시간 복잡도: O(VE)

플로이드-워셜 알고리즘(Floyd-Warshall Algorithm)
모든 정점 쌍 사이의 최단 경로를 찾는다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
# 플로이드-워셜 알고리즘 구현 예시
def floyd_warshall(graph):
    n = len(graph)
    dist = [row[:] for row in graph]  # 그래프의 인접 행렬 복사

    # k: 중간 정점
    for k in range(n):
        # i: 출발 정점
        for i in range(n):
            # j: 도착 정점
            for j in range(n):
                # i에서 k를 거쳐 j로 가는 경로가 더 짧은 경우 업데이트
                if dist[i][k] + dist[k][j] < dist[i][j]:
                    dist[i][j] = dist[i][k] + dist[k][j]

    return dist

시간 복잡도: O(V³)

최소 신장 트리(MST, Minimum Spanning Tree) 알고리즘

크루스칼 알고리즘(Kruskal’s Algorithm)
간선을 가중치 순으로 정렬한 후, Union-Find 자료구조를 사용하여 사이클을 형성하지 않는 간선만 선택한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 크루스칼 알고리즘 구현 예시
class DisjointSet:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 경로 압축
        return self.parent[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)

        if root_x == root_y:
            return

        # 랭크를 기준으로 합치기 (Union by Rank)
        if self.rank[root_x] < self.rank[root_y]:
            self.parent[root_x] = root_y
        else:
            self.parent[root_y] = root_x
            if self.rank[root_x] == self.rank[root_y]:
                self.rank[root_x] += 1

def kruskal(graph):
    n = graph.V
    result = []  # MST를 구성할 간선 리스트

    # 간선을 가중치 기준으로 정렬
    sorted_edges = sorted(graph.edges, key=lambda x: x[2])

    disjoint_set = DisjointSet(n)

    edge_count = 0
    for u, v, weight in sorted_edges:
        # 사이클을 형성하지 않는 경우에만 간선 추가
        if disjoint_set.find(u) != disjoint_set.find(v):
            disjoint_set.union(u, v)
            result.append((u, v, weight))
            edge_count += 1

            # MST는 정점 수 - 1개의 간선을 가짐
            if edge_count == n - 1:
                break

    return result

시간 복잡도: O(E log E) 또는 O(E log V)

프림 알고리즘(Prim’s Algorithm)
시작 정점에서부터 트리를 확장해 나가는 방식으로, 항상 최소 가중치 간선을 선택한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# 프림 알고리즘 구현 예시 (인접 행렬 사용)
import heapq

def prim(graph):
    n = len(graph)
    selected = [False] * n  # MST에 포함된 정점 표시
    result = []  # MST를 구성할 간선 리스트

    # 시작 정점 (0번 정점)
    selected[0] = True
    edge_count = 0

    # MST는 정점 수 - 1개의 간선을 가짐
    while edge_count < n - 1:
        minimum = float('inf')
        u, v = -1, -1

        # 이미 선택된 정점에서 선택되지 않은 정점으로 가는 최소 가중치 간선 찾기
        for i in range(n):
            if selected[i]:
                for j in range(n):
                    if not selected[j] and graph[i][j] > 0 and graph[i][j] < minimum:
                        minimum = graph[i][j]
                        u, v = i, j

        if u != -1 and v != -1:
            result.append((u, v, minimum))
            selected[v] = True
            edge_count += 1

    return result

개선된 프림 알고리즘(우선순위 큐 사용):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 개선된 프림 알고리즘 구현 예시 (인접 리스트 사용)
def prim_improved(graph):
    n = len(graph)
    selected = [False] * n
    result = []

    # 시작 정점 (0번 정점)
    priority_queue = [(0, 0, -1)]  # (가중치, 정점, 연결된 이전 정점)

    while priority_queue:
        weight, u, prev = heapq.heappop(priority_queue)

        if selected[u]:
            continue

        selected[u] = True

        if prev != -1:  # 시작 정점이 아닌 경우
            result.append((prev, u, weight))

        for v, w in graph[u]:
            if not selected[v]:
                heapq.heappush(priority_queue, (w, v, u))

    return result

시간 복잡도: O((V+E)log V) (최소 힙 사용 시)

그래프의 응용 분야

네트워크 분석
- 소셜 네트워크 분석
- 통신 네트워크 설계
- 웹 페이지 랭킹 (PageRank 알고리즘)
경로 찾기
- 내비게이션 시스템
- 로봇 경로 계획
- 네트워크 라우팅
스케줄링
- 작업 스케줄링
- 프로젝트 관리 (PERT/CPM)
생물학 및 화학
- 단백질 상호작용 네트워크
- 분자 구조 분석
인공지능
- 지식 표현
- 전문가 시스템
- 게임 트리 (미니맥스 알고리즘)

고급 그래프 알고리즘

강한 연결 요소(SCC, Strongly Connected Components)
- 타잔 알고리즘(Tarjan’s Algorithm)
- 코사라주 알고리즘(Kosaraju’s Algorithm)
위상 정렬(Topological Sort)
- 방향 비순환 그래프(DAG)에서 정점들을 선형으로 정렬하는 알고리즘
최대 유량 알고리즘(Maximum Flow)
- 포드-풀커슨 알고리즘(Ford-Fulkerson Algorithm)
- 에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)

그래프 (Graph)

그래프 (Graph)

그래프의 기본 개념

그래프의 종류

방향성에 따른 분류

가중치에 따른 분류

연결성에 따른 분류

순환성에 따른 분류

특수한 그래프

그래프의 표현 방법

인접 행렬(Adjacency Matrix)

인접 리스트(Adjacency List)

간선 리스트(Edge List)

그래프 탐색 알고리즘

최단 경로 알고리즘

최소 신장 트리(MST, Minimum Spanning Tree) 알고리즘

그래프의 응용 분야

고급 그래프 알고리즘

참고 및 출처

Fundamentals of Graph

Types of Graph

그래프 (Graph)#

그래프의 기본 개념#

그래프의 종류#

방향성에 따른 분류#

가중치에 따른 분류#

연결성에 따른 분류#

순환성에 따른 분류#

특수한 그래프#

그래프의 표현 방법#

인접 행렬(Adjacency Matrix)#

인접 리스트(Adjacency List)#

간선 리스트(Edge List)#

그래프 탐색 알고리즘#

최단 경로 알고리즘#

최소 신장 트리(MST, Minimum Spanning Tree) 알고리즘#

그래프의 응용 분야#

고급 그래프 알고리즘#

참고 및 출처#

그래프 (Graph)

그래프의 기본 개념

그래프의 종류

방향성에 따른 분류

가중치에 따른 분류

연결성에 따른 분류

순환성에 따른 분류

특수한 그래프

그래프의 표현 방법

인접 행렬(Adjacency Matrix)

인접 리스트(Adjacency List)

간선 리스트(Edge List)

그래프 탐색 알고리즘

최단 경로 알고리즘

최소 신장 트리(MST, Minimum Spanning Tree) 알고리즘

그래프의 응용 분야

고급 그래프 알고리즘

참고 및 출처