K-d Tree

K-d Tree는 k차원 공간에서 점들을 효율적으로 저장하고 검색하기 위한 이진 트리 기반의 공간 분할 데이터 구조로, K-d Tree는 k차원 공간을 재귀적으로 분할하여 표현하는 이진 트리이다.
각 노드는 k차원 공간의 한 점을 나타내며, 비단말 노드는 해당 차원을 기준으로 공간을 두 개의 하위 공간으로 분할한다.

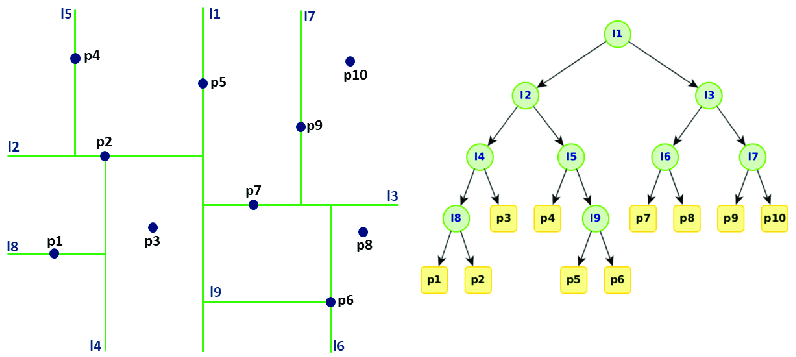
Visualization of the k-d tree algorithm
https://www.researchgate.net/figure/sualization-of-the-k-d-tree-algorithm_fig4_327289160

특징

  1. 다차원 데이터 처리: k차원 공간의 점들을 효율적으로 저장하고 검색할 수 있다.
  2. 계층적 구조: 공간을 재귀적으로 분할하여 계층적으로 표현한다.
  3. 차원 순환: 트리의 각 레벨마다 분할 기준이 되는 차원이 순환된다.
  4. 균형 구조: 중앙값을 기준으로 분할하여 균형 잡힌 트리를 구성한다.

장점

  1. 효율적인 검색: 다차원 공간에서의 근접 이웃 검색이나 범위 검색을 빠르게 수행할 수 있다.
  2. 차원 축소: 문제의 차원을 줄여 검색 시간을 단축하고 메모리 사용을 줄일 수 있다.
  3. 다양한 응용: 데이터 마이닝, 컴퓨터 그래픽스, 과학 계산 등 다양한 분야에 활용된다.

단점

  1. 고차원 데이터의 한계: 차원이 증가할수록 성능이 저하될 수 있다.
  2. 불균형 가능성: 데이터 분포에 따라 트리가 불균형해질 수 있다.
  3. 동적 데이터 처리의 어려움: 데이터 삽입/삭제 시 트리 재구성이 필요할 수 있다.

응용

  1. 최근접 이웃 검색: 머신러닝의 k-최근접 이웃(k-NN) 알고리즘에 활용된다.
  2. 범위 검색: 지리 정보 시스템(GIS)에서 특정 영역 내 객체 검색에 사용된다.
  3. 컴퓨터 비전: 이미지 처리와 특징점 매칭에 활용된다.
  4. 충돌 감지: 게임이나 시뮬레이션에서 객체 간 충돌 감지에 사용된다.

동작 원리

  1. 트리 구축:

    • 각 레벨에서 분할 축(차원)을 선택한다.
    • 선택된 축을 기준으로 데이터의 중앙값을 찾는다.
    • 중앙값을 기준으로 데이터를 좌우 하위 트리로 분할한다.
    • 이 과정을 재귀적으로 반복하여 트리를 구축한다.

  2. 검색:

    • 루트 노드부터 시작하여 검색 대상과 노드의 값을 비교한다.
    • 현재 레벨의 분할 축을 기준으로 좌우 서브트리 중 하나를 선택하여 탐색을 계속한다.
    • 리프 노드에 도달하거나 조건을 만족하는 노드를 찾을 때까지 이 과정을 반복한다.

구성 요소

  1. 노드: 각 노드는 k차원 점과 분할 축 정보를 저장한다.
  2. 분할 축: 각 레벨에서 공간을 분할하는 기준이 되는 차원을 나타낸다.
  3. 좌우 자식 노드: 분할된 하위 공간을 나타내는 노드들이다.

구현 방식

다음은 Python을 사용한 K-d Tree의 기본 구현 예시:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

class KDNode:
    def __init__(self, point, left=None, right=None):
        self.point = point
        self.left = left
        self.right = right

class KDTree:
    def __init__(self, points):
        self.root = self.build_kdtree(points, 0)

    def build_kdtree(self, points, depth):
        if not points:
            return None

        k = len(points[0])
        axis = depth % k

        points.sort(key=lambda x: x[axis])
        median = len(points) // 2

        return KDNode(
            point=points[median],
            left=self.build_kdtree(points[:median], depth + 1),
            right=self.build_kdtree(points[median + 1:], depth + 1)
        )

    def nearest_neighbor(self, target):
        def search(node, target, depth, best):
            if node is None:
                return best

            k = len(target)
            axis = depth % k

            next_best = min(best, node.point, key=lambda x: self.distance(target, x))
            next_branch = node.left if target[axis] < node.point[axis] else node.right
            other_branch = node.right if next_branch == node.left else node.left

            best = search(next_branch, target, depth + 1, next_best)

            if self.distance(target, best) > abs(target[axis] - node.point[axis]):
                best = search(other_branch, target, depth + 1, best)

            return best

        return search(self.root, target, 0, self.root.point)

    @staticmethod
    def distance(p1, p2):
        return sum((a - b) ** 2 for a, b in zip(p1, p2)) ** 0.5

# 사용 예시
points = [(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)]
kdtree = KDTree(points)
nearest = kdtree.nearest_neighbor((9, 2))
print(f"Nearest point to (9, 2): {nearest}")

이 구현은 K-d Tree의 기본 구조와 최근접 이웃 검색 기능을 보여줍니다. 실제 응용에서는 더 복잡한 기능과 최적화가 필요할 수 있다.

참고 및 출처