Splay Tree#
Splay Tree는 이진 검색 트리(Binary Search Tree)의 한 종류로, 데이터를 저장하고 효율적으로 검색, 삽입, 삭제할 수 있는 구조를 가지고 있다.
데이터베이스, 캐시 관리, 네트워크 라우팅 등 다양한 응용 분야에서 사용된다.
Splay Tree는 자체 균형 이진 검색 트리의 일종으로, 최근에 접근한 노드를 루트로 이동시키는 “splay” 연산을 통해 자가 조정되는 특징을 가진다.
- 자체 균형: splay 연산을 통해 트리의 균형을 유지한다.
- 최근 접근 노드 최적화: 자주 접근하는 노드를 루트 근처로 이동시켜 빠른 접근을 가능하게 한다.
- 동적 구조: 삽입, 삭제, 검색 연산 후 트리 구조가 변경된다.
- 구현이 상대적으로 단순하다.
- 자주 접근하는 데이터에 대해 빠른 접근 속도를 제공한다.
- 추가적인 균형 정보 저장이 필요 없다.
- 최악의 경우 트리의 높이가 O(n)이 될 수 있다.
- 연산마다 트리 구조가 변경되어 예측이 어려울 수 있다.
- 캐시 관리: 최근 접근 데이터의 빠른 검색에 활용.
- 네트워크 라우팅: IP 라우팅 테이블 관리.
- 자동 완성 및 검색 엔진: 빠른 검색 결과 제공.
- Garbage Collector 알고리즘.
동작 원리#
Splay Tree의 핵심 동작은 “splay” 연산이다.
이 연산은 다음과 같은 단계로 이루어진다:
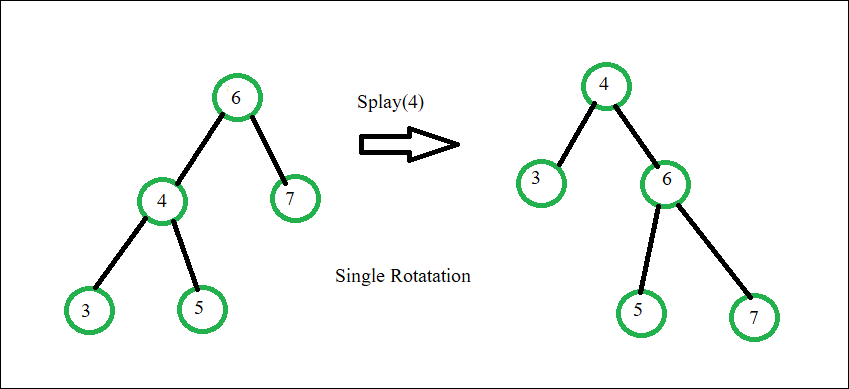
- Zig:
- 대상 노드가 루트의 직접적인 자식일 때 사용.
- 단순한 회전으로 대상 노드를 루트로 만듦.
 Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
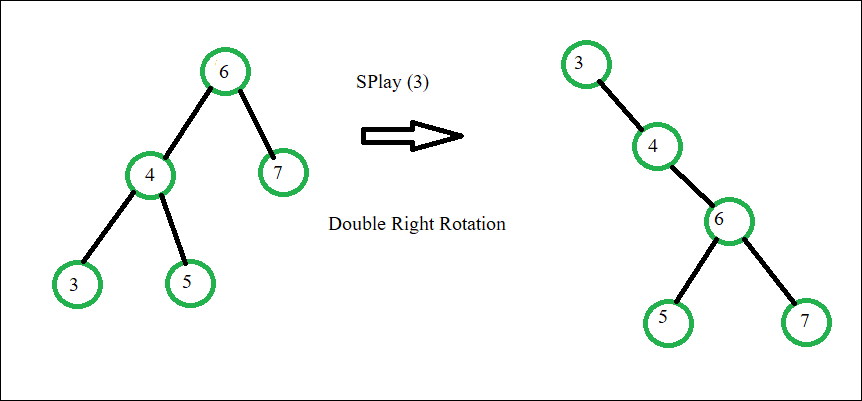
- Zig-Zig:
- 대상 노드와 그 부모가 같은 방향(둘 다 왼쪽 또는 둘 다 오른쪽)일 때.
- 부모를 먼저 회전한 후 대상 노드를 회전.
 Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
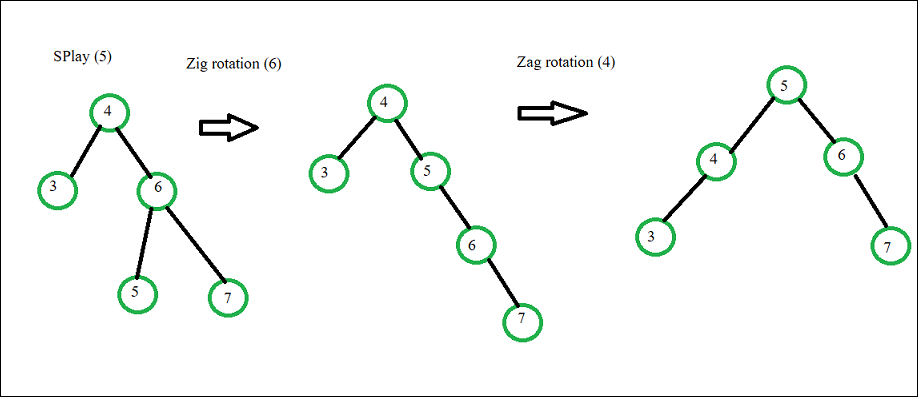
- Zig-Zag:
- 대상 노드와 그 부모가 다른 방향일 때.
- 대상 노드를 두 번 회전하여 루트로 만듦.
 Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
Source: https://www.geeksforgeeks.org/introduction-to-splay-tree-data-structure/
이 과정을 통해 접근한 노드가 루트로 이동한다.
구성 요소#
- 노드: 키 값과 왼쪽, 오른쪽 자식 노드에 대한 참조를 포함한다.
- 루트: 트리의 최상위 노드이다.
- 회전 연산: 트리의 구조를 변경하는 기본 연산이다.
구현 방식#
Splay Tree는 일반적으로 다음과 같은 방식으로 구현된다:
- 노드 구조체 정의: 키 값, 왼쪽/오른쪽 자식 노드 참조, (선택적으로) 부모 노드 참조를 포함.
- 회전 연산 구현: 왼쪽 회전, 오른쪽 회전 함수 구현.
- Splay 연산 구현: Zig, Zig-Zig, Zig-Zag 케이스 처리.
- 삽입, 삭제, 검색 연산 구현: 각 연산 후 splay 연산 수행.
주요 연산들의 동작 과정#
검색 연산:
- 일반적인 이진 검색 트리처럼 검색을 수행합니다
- 찾은 노드를 splaying하여 루트로 만듭니다
- 검색 실패시에도 마지막으로 접근한 노드를 splaying합니다
삽입 연산:
- 일반적인 이진 검색 트리처럼 삽입 위치를 찾습니다
- 새 노드를 삽입합니다
- 삽입된 노드를 splaying하여 루트로 만듭니다
삭제 연산:
- 삭제할 노드를 찾아 splaying합니다
- 왼쪽 서브트리의 최대값을 찾아 splaying합니다
- 오른쪽 서브트리를 새로운 루트의 오른쪽에 붙입니다
예시 코드 (Python)#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
class SplayTree:
def __init__(self):
self.root = None
def rotate_right(self, x):
y = x.left
x.left = y.right
y.right = x
return y
def rotate_left(self, x):
y = x.right
x.right = y.left
y.left = x
return y
def splay(self, root, key):
if not root or root.key == key:
return root
if root.key > key:
if not root.left:
return root
if root.left.key > key:
root.left.left = self.splay(root.left.left, key)
root = self.rotate_right(root)
elif root.left.key < key:
root.left.right = self.splay(root.left.right, key)
if root.left.right:
root.left = self.rotate_left(root.left)
return self.rotate_right(root) if root.left else root
else:
if not root.right:
return root
if root.right.key > key:
root.right.left = self.splay(root.right.left, key)
if root.right.left:
root.right = self.rotate_right(root.right)
elif root.right.key < key:
root.right.right = self.splay(root.right.right, key)
root = self.rotate_left(root)
return self.rotate_left(root) if root.right else root
def insert(self, key):
if not self.root:
self.root = Node(key)
return
self.root = self.splay(self.root, key)
if self.root.key == key:
return
new_node = Node(key)
if self.root.key > key:
new_node.right = self.root
new_node.left = self.root.left
self.root.left = None
else:
new_node.left = self.root
new_node.right = self.root.right
self.root.right = None
self.root = new_node
def search(self, key):
if not self.root:
return None
self.root = self.splay(self.root, key)
return self.root.key if self.root.key == key else None
|
참고 및 출처#


