스택 (Stack)

스택 (Stack)

스택은 ‘쌓아올린 더미’라는 의미를 가진 자료구조로, 데이터를 차곡차곡 쌓아 올리는 형태를 취한다. 실생활에서 접시를 쌓아두거나 책을 쌓아두는 방식과 유사하다.
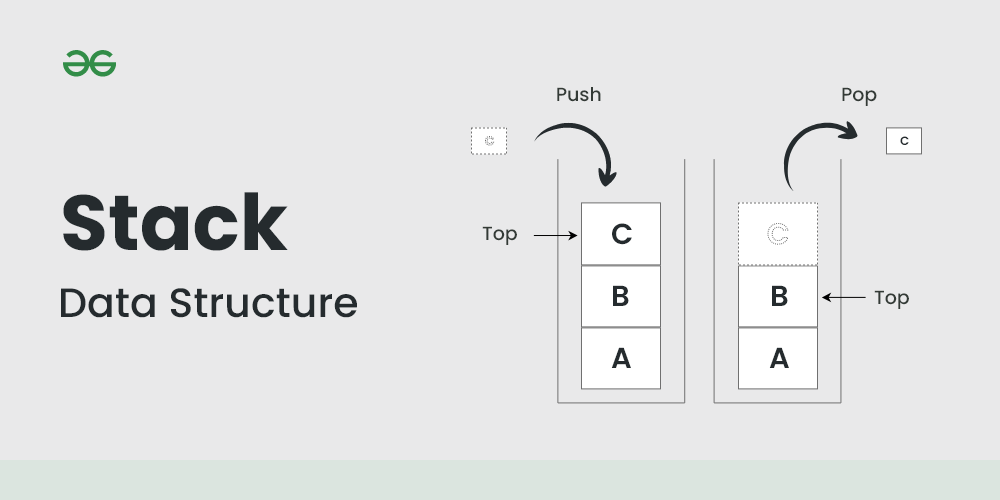
스택은 데이터의 삽입과 삭제가 한쪽 끝(스택의 상단 또는 top)에서만 이루어지는 제한적인 자료구조이다.

스택은 단순하지만 강력한 자료구조로, 다양한 알고리즘과 시스템에서 핵심적인 역할을 한다.
LIFO 특성을 활용하여 함수 호출 관리, 수식 계산, 구문 분석 등 다양한 문제를 효율적으로 해결할 수 있다.
스택의 모든 기본 연산이 O(1) 시간 복잡도를 가지므로 성능이 중요한 애플리케이션에서도 유용하게 사용된다.

스택은 배열이나 연결 리스트로 구현할 수 있으며, 각 구현 방식은 고유한 장단점을 가진다.
구현 방식의 선택은 메모리 사용량, 성능 요구사항, 동적 크기 조정 필요성 등을 고려하여 결정해야 한다.

스택의 특성

LIFO(Last In, First Out)

스택의 가장 중요한 특성은 LIFO(Last In, First Out), 즉 ‘후입선출’ 원칙이다.
이는 가장 마지막에 들어온 데이터가 가장 먼저 나가는 구조를 의미한다.
책상 위에 책을 쌓고, 맨 위의 책부터 하나씩 들어 올린다고 생각하면 쉽게 이해할 수 있다.

스택의 기본 연산

스택은 다음과 같은 기본 연산들을 제공한다:

1. push(item): 스택의 맨 위에 새로운 항목을 추가한다.
2. pop(): 스택의 맨 위에 있는 항목을 제거하고 반환한다.
3. peek()/top(): 스택의 맨 위 항목을 제거하지 않고 반환한다.
4. isEmpty(): 스택이 비어있는지 확인한다.
5. size(): 스택에 들어있는 항목의 개수를 반환한다.

스택의 상태

스택에는 두 가지 특별한 상태가 있다:

• 스택 언더플로우(Stack Underflow): 비어있는 스택에서 pop 연산을 시도할 때 발생한다.
• 스택 오버플로우(Stack Overflow): 스택이 꽉 찼을 때 push 연산을 시도할 때 발생한다. (배열로 구현된 스택에서 주로 발생)

이러한 문제들을 방지하기 위해서는 push 연산 전에 스택이 가득 찼는지, pop 연산 전에 스택이 비어있는지 확인하는 것이 중요하다. 적절한 에러 처리와 예외 처리를 통해 프로그램의 안정성을 높일 수 있다.

스택의 구현 방법

스택은 다양한 방법으로 구현할 수 있다.
가장 일반적인 두 가지 방법은 배열과 연결 리스트를 사용하는 것이다.

배열을 이용한 스택 구현

배열은 메모리에 연속적인 공간을 할당받아 사용하므로, 인덱스를 통한 접근이 빠르고 구현이 간단하다.

장점:

• 구현이 간단하다.
• 인덱스를 통한 접근으로 peek 연산이 O(1)로 빠르다.
• 메모리 사용량이 예측 가능하다.

단점:

• 최대 크기가 미리 정해져야 한다.
• 크기를 초과하면 스택 오버플로우가 발생한다.
• 크기를 너무 크게 잡으면 메모리 낭비가 발생할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

# Python으로 구현한 배열 기반 스택
class ArrayStack:
    def __init__(self, capacity=10):
        self.items = [None] * capacity  # 고정 크기 배열 초기화
        self.top = -1  # 스택의 top 인덱스 (비어있을 때는 -1)
        self.capacity = capacity
    
    def is_empty(self):
        return self.top == -1
    
    def is_full(self):
        return self.top == self.capacity - 1
    
    def push(self, item):
        if self.is_full():
            raise Exception("스택 오버플로우")
        self.top += 1
        self.items[self.top] = item
    
    def pop(self):
        if self.is_empty():
            raise Exception("스택 언더플로우")
        item = self.items[self.top]
        self.items[self.top] = None  # 참조 제거
        self.top -= 1
        return item
    
    def peek(self):
        if self.is_empty():
            raise Exception("스택이 비어있습니다")
        return self.items[self.top]
    
    def size(self):
        return self.top + 1

동적 배열을 이용한 스택 구현

용량 제한 문제를 해결하기 위해 필요에 따라 크기가 자동으로 조정되는 동적 배열을 사용할 수 있다.

장점:

• 크기 제한이 없다.
• 필요에 따라 자동으로 크기가 조정된다.

단점:

• 배열 확장 시 메모리 재할당과 복사가 발생하여 가끔 O(n) 시간이 소요될 수 있다.
• 평균적인 성능은 여전히 O(1)이다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# Python으로 구현한 동적 배열 기반 스택
class DynamicArrayStack:
    def __init__(self):
        self.items = []  # 동적 배열 사용
    
    def is_empty(self):
        return len(self.items) == 0
    
    def push(self, item):
        self.items.append(item)  # 배열 끝에 추가
    
    def pop(self):
        if self.is_empty():
            raise Exception("스택 언더플로우")
        return self.items.pop()  # 배열 끝에서 제거 및 반환
    
    def peek(self):
        if self.is_empty():
            raise Exception("스택이 비어있습니다")
        return self.items[-1]  # 배열의 마지막 요소 반환
    
    def size(self):
        return len(self.items)

연결 리스트를 이용한 스택 구현

연결 리스트는 노드들이 포인터로 연결되어 있는 구조로, 크기 제한이 없고 동적으로 메모리를 할당받는다.

장점:

• 크기 제한이 없다.
• 동적 메모리 할당으로 메모리를 효율적으로 사용한다.
• 삽입과 삭제가 항상 O(1) 시간에 수행된다.

단점:

• 포인터 저장으로 인한 추가 메모리 오버헤드가 있다.
• 포인터를 따라가야 하기 때문에 캐시 효율성이 배열보다 떨어질 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# Python으로 구현한 연결 리스트 기반 스택
class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

class LinkedListStack:
    def __init__(self):
        self.top = None  # 스택의 맨 위 노드
        self.size_count = 0  # 스택 크기 카운터
    
    def is_empty(self):
        return self.top is None
    
    def push(self, item):
        new_node = Node(item)
        new_node.next = self.top  # 새 노드가 현재 top을 가리키게 함
        self.top = new_node  # top이 새 노드를 가리키게 함
        self.size_count += 1
    
    def pop(self):
        if self.is_empty():
            raise Exception("스택 언더플로우")
        item = self.top.data
        self.top = self.top.next  # top을 다음 노드로 이동
        self.size_count -= 1
        return item
    
    def peek(self):
        if self.is_empty():
            raise Exception("스택이 비어있습니다")
        return self.top.data
    
    def size(self):
        return self.size_count

스택 연산의 시간 복잡도

일반적으로 모든 스택 연산(push, pop, peek, isEmpty, size)은 O(1), 즉 상수 시간에 수행된다.
이는 스택이 항상 맨 위의 요소에만 접근하기 때문이다.

• push: O(1) - 단, 동적 배열의 경우 가끔 O(n)이 될 수 있음
• pop: O(1) - 단, 동적 배열의 경우 가끔 O(n)이 될 수 있음
• peek: O(1)
• isEmpty: O(1)
• size: O(1)

스택의 응용 분야

스택은 다양한 알고리즘과 응용 프로그램에서 사용된다.

프로그래밍 언어와 컴파일러

1. 함수 호출 관리: 프로그램 실행 시 함수 호출과 반환을 관리하는 호출 스택(call stack)
2. 지역 변수 관리: 함수 내의 지역 변수 저장
3. 인터프리터/컴파일러: 수식 계산, 구문 분석 등에 활용

알고리즘

1. 괄호 매칭 검사: ‘(’, ‘{’, ‘[’ 등의 열린 괄호를 스택에 넣고, 닫힌 괄호 ‘)’, ‘}’, ‘]‘를 만날 때 스택에서 꺼내어 쌍이 맞는지 확인

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   def is_balanced(expression): stack = [] brackets = {'(': ')', '{': '}', '[': ']'} for char in expression: if char in brackets: # 여는 괄호면 스택에 추가 stack.append(char) elif char in brackets.values(): # 닫는 괄호면 if not stack: # 스택이 비어있으면 불균형 return False top = stack.pop() if brackets[top] != char: # 괄호 쌍이 맞지 않으면 불균형 return False return len(stack) == 0 # 스택이 비어있어야 모든 괄호가 매칭됨

2. 역폴란드 표기법(후위 표기법) 계산:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

   def evaluate_postfix(expression): stack = [] tokens = expression.split() for token in tokens: if token.isdigit(): # 숫자면 스택에 추가 stack.append(int(token)) else: # 연산자면 스택에서 두 숫자를 꺼내 계산 후 결과를 다시 스택에 추가 b = stack.pop() a = stack.pop() if token == '+': stack.append(a + b) elif token == '-': stack.append(a - b) elif token == '*': stack.append(a * b) elif token == '/': stack.append(a / b) return stack.pop() # 최종 결과는 스택에 남은 값 # 예시: "2 3 + 4 *" = (2 + 3) * 4 = 20 print(evaluate_postfix("2 3 + 4 *")) # 출력: 20

3. 중위 표기법에서 후위 표기법으로 변환:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

   def infix_to_postfix(expression): precedence = {'+': 1, '-': 1, '*': 2, '/': 2, '^': 3} stack = [] result = [] tokens = expression.split() for token in tokens: if token.isalnum(): # 피연산자(숫자나 변수)면 결과에 추가 result.append(token) elif token == '(': # 여는 괄호면 스택에 추가 stack.append(token) elif token == ')': # 닫는 괄호면 여는 괄호를 만날 때까지 스택의 연산자를 결과에 추가 while stack and stack[-1] != '(': result.append(stack.pop()) stack.pop() # '('를 스택에서 제거 else: # 연산자면 # 스택 top에 있는 연산자의 우선순위가 현재 연산자보다 높거나 같으면 pop while stack and stack[-1] != '(' and precedence.get(stack[-1], 0) >= precedence.get(token, 0): result.append(stack.pop()) stack.append(token) # 현재 연산자를 스택에 추가 # 스택에 남아있는 연산자를 모두 결과에 추가 while stack: result.append(stack.pop()) return ' '.join(result) # 예시: "a + b * c" -> "a b c * +" print(infix_to_postfix("a + b * c")) # 출력: "a b c * +"

4. 백트래킹 알고리즘: DFS(깊이 우선 탐색)에서 방문 경로를 저장

5. 히스토리 관리: 웹 브라우저의 뒤로 가기/앞으로 가기 기능

유명한 스택 기반 문제들

1. 히스토그램에서 가장 큰 직사각형 찾기

2. 단조 증가/감소 스택을 이용한 다양한 문제 해결

3. 스택을 이용한 O(1) 시간 내 최소값 찾기

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

   # O(1) 시간에 최소값을 찾는 스택 class MinStack: def __init__(self): self.stack = [] # (값, 현재까지의 최소값) 쌍을 저장 def push(self, val): # 스택이 비어있으면 val이 최소값, 아니면 현재 최소값과 val 중 작은 값이 최소값 current_min = val if self.is_empty() else min(val, self.get_min()) self.stack.append((val, current_min)) def pop(self): if self.is_empty(): raise Exception("스택 언더플로우") return self.stack.pop()[0] # 값만 반환 def top(self): if self.is_empty(): raise Exception("스택이 비어있습니다") return self.stack[-1][0] # 값만 반환 def get_min(self): if self.is_empty(): raise Exception("스택이 비어있습니다") return self.stack[-1][1] # 최소값 반환 def is_empty(self): return len(self.stack) == 0

스택과 재귀의 관계

재귀(recursion)는 함수가 자기 자신을 호출하는 프로그래밍 기법이다.
모든 재귀 함수는 내부적으로 시스템 스택을 사용한다.

1
2
3
4
5

# 재귀를 이용한 팩토리얼 계산
def factorial(n):
    if n <= 1:  # 기저 조건
        return 1
    return n * factorial(n-1)  # 재귀 호출

위 코드의 실행 과정을 스택으로 표현하면:

1. factorial(3) 호출 → 스택에 factorial(3) 함수 프레임 추가
2. factorial(2) 호출 → 스택에 factorial(2) 함수 프레임 추가
3. factorial(1) 호출 → 스택에 factorial(1) 함수 프레임 추가
4. factorial(1)은 1 반환 → factorial(1) 함수 프레임 제거
5. factorial(2)는 2 * 1 = 2 반환 → factorial(2) 함수 프레임 제거
6. factorial(3)는 3 * 2 = 6 반환 → factorial(3) 함수 프레임 제거

재귀를 반복문과 스택으로 변환

모든 재귀 함수는 스택과 반복문을 사용하여 비재귀적으로 구현할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# 스택을 이용한 팩토리얼 계산 (비재귀적 방법)
def factorial_iterative(n):
    if n <= 1:
        return 1
    
    stack = []
    while n > 1:
        stack.append(n)
        n -= 1
    
    result = 1
    while stack:
        result *= stack.pop()
    
    return result

스택의 변형 및 확장

이중 스택 (Double Stack)

하나의 배열을 사용하여 두 개의 스택을 구현하는 방식이다.
배열의 양쪽 끝에서 시작하여 중앙을 향해 성장한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class DoubleStack:
    def __init__(self, capacity):
        self.items = [None] * capacity
        self.top1 = -1  # 첫 번째 스택의 top (왼쪽에서 오른쪽으로 성장)
        self.top2 = capacity  # 두 번째 스택의 top (오른쪽에서 왼쪽으로 성장)
        self.capacity = capacity
    
    def is_full(self):
        return self.top1 + 1 == self.top2
    
    def is_empty1(self):
        return self.top1 == -1
    
    def is_empty2(self):
        return self.top2 == self.capacity
    
    def push1(self, item):
        if self.is_full():
            raise Exception("스택 오버플로우")
        self.top1 += 1
        self.items[self.top1] = item
    
    def push2(self, item):
        if self.is_full():
            raise Exception("스택 오버플로우")
        self.top2 -= 1
        self.items[self.top2] = item
    
    def pop1(self):
        if self.is_empty1():
            raise Exception("스택1 언더플로우")
        item = self.items[self.top1]
        self.items[self.top1] = None
        self.top1 -= 1
        return item
    
    def pop2(self):
        if self.is_empty2():
            raise Exception("스택2 언더플로우")
        item = self.items[self.top2]
        self.items[self.top2] = None
        self.top2 += 1
        return item

기타 스택 변형

1. 우선순위가 있는 스택: 요소마다 우선순위를 부여하고, 삭제 시 우선순위가 가장 높은 요소를 제거
2. 스택 집합(Stack Set): 여러 개의 스택을 하나의 논리적 단위로 관리

스택의 실제 시스템 응용

메모리 관리와 프로세스

1. 프로그램 실행 메모리: 스택 세그먼트, 힙 세그먼트, 데이터 세그먼트, 코드 세그먼트로 구성
2. 스택 세그먼트: 함수 호출 정보, 지역 변수, 반환 주소 등을 저장
3. 스택 프레임: 함수 호출마다 생성되는 메모리 블록으로, 함수의 매개변수, 지역 변수, 반환 주소 등 포함

운영 체제에서의 스택

1. 인터럽트 처리: CPU가 인터럽트를 처리할 때 현재 상태를 스택에 저장
2. 멀티태스킹: 프로세스나 스레드 간 문맥 전환(context switching) 시 상태 정보 저장

웹 브라우저 및 애플리케이션

1. 브라우저 히스토리: 뒤로가기/앞으로가기 기능
2. 실행 취소/다시 실행(Undo/Redo): 문서 편집기에서의 작업 기록 관리
3. JS 이벤트 루프: 이벤트 처리와 비동기 호출 관리

스택 구현 시 주의할 점

1. 스택 오버플로우 처리: 고정 크기 스택의 경우 범위를 벗어나지 않도록 주의
2. 스택 언더플로우 처리: 빈 스택에서 pop 연산 시 적절한 에러 처리
3. 메모리 누수 방지: 참조형 데이터를 사용할 때 pop 시 참조 해제
4. 스레드 안전성: 멀티스레드 환경에서 동시성 제어

참고 및 출처