큐 (Queue)
큐는 컴퓨터 과학에서 가장 기본적이고 중요한 자료구조 중 하나이다.
일상생활에서 은행 창구나 매표소의 대기열과 같은 개념으로, 컴퓨터 과학에서도 데이터를 순서대로 처리하는 다양한 상황에 활용된다.
큐는 데이터를 일정한 순서에 따라 저장하고 접근하는 선형 자료구조이다.
큐의 가장 큰 특징은 데이터가 들어온 순서대로 처리된다는 점이다.
큐는 단순하면서도 강력한 자료구조로, 다양한 알고리즘과 시스템에서 핵심적인 역할을 한다.
FIFO 특성을 활용하여 작업 스케줄링, 버퍼링, 그래프 탐색 등 다양한 문제를 효율적으로 해결할 수 있다.
큐는 배열, 연결 리스트, 또는 이중 스택 등 다양한 방식으로 구현할 수 있으며, 각 구현 방식은 고유한 장단점을 가진다.
응용 분야와 요구사항에 따라 적절한 큐 구현을 선택하는 것이 중요하다.
큐는 우선순위 큐, 덱, 원형 버퍼 등 다양한 변형으로 확장되어 더 넓은 범위의 문제를 해결할 수 있다.
분산 시스템, 멀티스레딩, 실시간 데이터 처리 등 현대적인 컴퓨팅 환경에서도 큐의 개념은 여전히 중요한 역할을 한다.
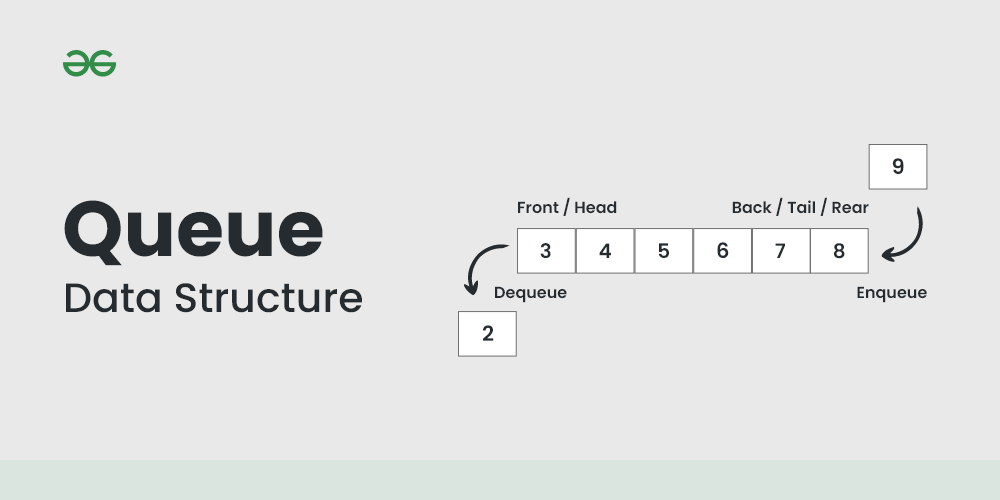
큐의 특성
FIFO(First In, First Out)
큐의 핵심 특성은 FIFO(First In, First Out), 즉 ‘선입선출’ 원칙이다.
이는 가장 먼저 들어온 데이터가 가장 먼저 나가는 구조를 의미한다.
마치 줄을 서서 기다리는 사람들이 도착한 순서대로 서비스를 받는 것과 같은 원리이다.
큐의 용어
큐에서는 다음과 같은 용어들이 사용된다:
- Front(또는 Head): 큐의 맨 앞, 즉 가장 오래된 데이터가 위치한 곳으로 데이터가 제거되는 위치
- Rear(또는 Tail): 큐의 맨 뒤, 즉 가장 최근에 추가된 데이터가 위치한 곳으로 새 데이터가 추가되는 위치
- Enqueue: 큐의 rear에 새로운 데이터를 추가하는 연산
- Dequeue: 큐의 front에서 데이터를 제거하고 반환하는 연산
큐의 기본 연산
큐는 다음과 같은 기본 연산들을 제공한다:
- enqueue(item): 큐의 rear에 새로운 항목을 추가한다.
- dequeue(): 큐의 front에 있는 항목을 제거하고 반환한다.
- peek()/front(): 큐의 front 항목을 제거하지 않고 반환한다.
- isEmpty(): 큐가 비어있는지 확인한다.
- size(): 큐에 들어있는 항목의 개수를 반환한다.
큐의 상태
큐에는 두 가지 특별한 상태가 있다:
- 큐 언더플로우(Queue Underflow): 비어있는 큐에서 dequeue 연산을 시도할 때 발생한다.
- 큐 오버플로우(Queue Overflow): 고정 크기 큐가 꽉 찼을 때 enqueue 연산을 시도할 때 발생한다.
큐의 구현 방법
큐는 다양한 방법으로 구현할 수 있다.
가장 일반적인 구현 방법으로는 배열, 연결 리스트, 그리고 원형 큐가 있다.
배열을 이용한 큐 구현
배열을 사용하여 큐를 구현하는 가장 단순한 방법이다.
front와 rear 인덱스를 사용하여 큐의 시작과 끝을 추적한다.
장점:
- 구현이 비교적 간단하다.
- 인덱스를 통한 접근으로 peek 연산이 O(1)로 빠르다.
- 메모리 사용량이 예측 가능하다.
단점:
- 최대 크기가 미리 정해져야 한다.
- 단순 배열 구현에서는 dequeue 후 앞부분에 생기는 빈 공간을 활용하지 못하는 문제가 있다. (이는 원형 큐로 해결 가능)
| |
원형 큐(Circular Queue)
원형 큐는 일반 배열 기반 큐의 공간 낭비 문제를 해결하기 위한 변형이다.
배열의 끝에 도달하면 다시 배열의 처음으로 돌아가는 원형 개념을 사용한다.
위의 코드에서 이미 원형 큐 개념을 적용((index + 1) % capacity 연산을 통해).
동적 배열을 이용한 큐 구현
자바스크립트 배열이나 파이썬 리스트와 같은 동적 배열을 사용하면 크기 제한 없이 큐를 구현할 수 있다.
장점:
- 크기 제한이 없다.
- 구현이 매우 단순하다.
단점:
- dequeue 연산이 O(n) 시간이 소요된다. (배열의 첫 요소를 제거하면 나머지 모든 요소를 한 칸씩 이동시켜야 함)
- 큐의 크기가 커질수록 성능이 저하될 수 있다.
| |
연결 리스트를 이용한 큐 구현
연결 리스트는 동적으로 노드를 추가하고 제거할 수 있어 큐 구현에 적합하다.
장점:
- 크기 제한이 없다.
- 모든 연산(enqueue, dequeue, peek)이 O(1) 시간에 수행된다.
- 동적 메모리 할당으로 메모리를 효율적으로 사용한다.
단점:
- 포인터 저장으로 인한 추가 메모리 오버헤드가 있다.
- 포인터를 따라가야 하기 때문에 캐시 효율성이 배열보다 떨어질 수 있다.
| |
두 개의 스택을 이용한 큐 구현
흥미로운 접근 방식으로, 두 개의 스택을 사용하여 큐를 구현할 수도 있다.
작동 원리:
- enqueue: 항상 stack_in에 데이터를 추가합니다.
- dequeue:
- stack_out이 비어있지 않으면 stack_out에서 pop 연산을 수행한다.
- stack_out이 비어있으면 stack_in의 모든 항목을 stack_out으로 이동시킨 후(이 과정에서 순서가 뒤집힘), stack_out에서 pop 연산을 수행한다.
분석:
- enqueue 연산은 항상 O(1) 시간이 소요된다.
- dequeue 연산은 대부분의 경우 O(1)이지만, stack_out이 비어있을 때는 O(n) 시간이 소요된다.
- 평균적으로는 각 요소가 한 번만 이동하므로 분할 상환 분석(amortized analysis)에 따르면 dequeue 연산도 O(1)이다.
| |
큐 연산의 시간 복잡도
구현 방식에 따른 큐 연산의 시간 복잡도는 다음과 같다:
| 연산 | 연결 리스트 기반 큐 | 배열(원형 큐) 기반 큐 | 동적 배열 기반 큐 | 두 개의 스택 기반 큐 |
|---|---|---|---|---|
| enqueue | O(1) | O(1) | 평균 O(1), 최악 O(n) (배열 확장 시) | 평균 O(1), 최악 O(n) (배열 확장 시) |
| dequeue | O(1) | O(1) | O(n) (모든 요소를 한 칸씩 이동) | 분할 상환 O(1), 최악 O(n) |
| peek | O(1) | O(1) | O(1) | 분할 상환 O(1), 최악 O(n) |
| isEmpty | O(1) | O(1) | O(1) | O(1) |
| size | O(1) | O(1) | O(1) | O(1) |
큐의 변형
우선순위 큐(Priority Queue)
우선순위 큐는 각 요소에 우선순위가 할당되어 있고, 우선순위가 높은 요소가 먼저 처리되는 큐이다.
FIFO 규칙을 따르지 않고 우선순위에 따라 요소가 정렬된다.
- 우선순위 큐의 응용 분야
- 작업 스케줄링
- 네트워크 트래픽 관리(QoS)
- 다익스트라 알고리즘과 같은 그래프 알고리즘
- 사건 기반 시뮬레이션
| |
우선순위 큐는 주로 힙(Heap) 자료구조를 사용하여 구현된다.
힙은 완전 이진 트리로, 부모 노드의 값이 자식 노드의 값보다 항상 크거나(최대 힙) 작은(최소 힙) 특성을 가진다.
덱(Deque, Double-ended Queue)
덱은 양쪽 끝에서 모두 삽입과 삭제가 가능한 큐의 확장된 형태이다.
- 덱의 응용 분야
- 스택과 큐의 기능을 모두 필요로 하는 경우
- 회문(palindrome) 검사
- 슬라이딩 윈도우 문제
- 작업 스케줄링(작업 훔치기 알고리즘 등)
| |
원형 버퍼(Circular Buffer)
원형 버퍼는 고정된 크기의 버퍼에서 데이터를 순환시키는 FIFO 자료구조이다.
메모리를 재사용함으로써 효율적인 공간 활용이 가능하다.
- 원형 버퍼의 응용 분야
- 데이터 스트리밍(오디오, 비디오 버퍼링)
- 로그 저장
- 네트워크 패킷 버퍼링
- 프로듀서-컨슈머 패턴 구현
| |
큐 변형별 특성 비교표
| 큐 변형 | 특성 | 연산 | 주요 응용 분야 | 구현 복잡도 |
|---|---|---|---|---|
| 일반 큐 (Queue) | • FIFO (선입선출) • 한쪽 끝에서 삽입, 다른 쪽 끝에서 삭제 | • enqueue: 끝에 추가 • dequeue: 앞에서 제거 • peek: 앞 요소 조회 | • BFS • 작업 스케줄링 • 버퍼링 • 프린트 스풀링 | 낮음 |
| 우선순위 큐 (Priority Queue) | • 우선순위에 따라 요소 처리 • FIFO 규칙을 따르지 않음 • 주로 힙으로 구현 | • enqueue_with_priority • dequeue_highest • peek_highest | • 다익스트라 알고리즘 • 사건 기반 시뮬레이션 • 작업 스케줄링 • 네트워크 트래픽 관리 | 중간 |
| 덱 (Deque) | • 양쪽 끝에서 모두 삽입/삭제 가능 • 큐와 스택의 기능 결합 • 주로 이중 연결 리스트로 구현 | • add_front/add_rear • remove_front/remove_rear • peek_front/peek_rear | • 회문 검사 • 슬라이딩 윈도우 • 작업 스케줄링 • 스크롤 기록 유지 | 중간 |
| 원형 버퍼 (Circular Buffer) | • 고정 크기 메모리 재사용 • 메모리 효율적 FIFO 구현 • 덮어쓰기 옵션 가능 | • write: 데이터 쓰기 • read: 데이터 읽기 • peek: 데이터 확인 | • 스트리밍 데이터 • 로그 저장 • 네트워크 패킷 버퍼링 • 오디오/비디오 처리 | 중간 |
| 블로킹 큐 (Blocking Queue) | • 큐가 비었을 때 dequeue 호출 시 블로킹 • 큐가 가득 찼을 때 enqueue 호출 시 블로킹 • 스레드 간 동기화 | • put: 데이터 넣기(블로킹) • take: 데이터 가져오기(블로킹) • offer: 데이터 넣기(비블로킹) • poll: 데이터 가져오기(비블로킹) | • 프로듀서-컨슈머 패턴 • 스레드 풀 • 작업 대기열 • 멀티스레드 애플리케이션 | 높음 |
| 지연 큐 (Delay Queue) | • 각 요소가 지정된 지연 시간 이후에만 사용 가능 • 시간 기반 처리 • 우선순위 큐 기반 구현 | • offer: 지연 요소 추가 • take: 지연 만료된 요소 가져오기 • peek: 다음 만료 예정 요소 조회 | • 스케줄링 • 타임아웃 처리 • 캐시 만료 • 알림/미리 알림 | 높음 |
| 분산 큐 (Distributed Queue) | • 여러 노드에 분산된 큐 • 고가용성과 확장성 • 메시지 지속성 | • send: 메시지 전송 • receive: 메시지 수신 • acknowledge: 메시지 확인 | • 마이크로서비스 통신 • 이벤트 소싱 • 대규모 시스템 간 통신 • 비동기 작업 처리 | 매우 높음 |
큐의 응용 분야
큐는 다양한 알고리즘과 시스템에서 활용된다.
운영체제
- 프로세스 스케줄링: CPU 사용을 기다리는 프로세스들을 관리하기 위한 준비 큐(ready queue)
- 인터럽트 처리: 인터럽트를 처리하기 위한 인터럽트 큐
- 프린터 스풀링: 인쇄 작업을 관리하기 위한 인쇄 큐
- I/O 버퍼: 입출력 장치와 CPU 간의 속도 차이를 완화하기 위한 버퍼
네트워크
- 패킷 큐잉: 라우터나 스위치에서 패킷을 처리하기 위한 큐
- 서비스 큐: 웹 서버에서 클라이언트 요청을 처리하기 위한 큐
- 메시지 큐: 분산 시스템에서 비동기 통신을 위한 메시지 큐잉 시스템(RabbitMQ, Kafka 등)
알고리즘
너비 우선 탐색(BFS): 그래프나 트리를 레벨별로 탐색하는 알고리즘
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30# 큐를 이용한 BFS 구현 from collections import deque def bfs(graph, start): visited = set() # 방문한 노드 추적 queue = deque([start]) # 시작 노드를 큐에 추가 visited.add(start) while queue: node = queue.popleft() # 큐에서 노드 제거 print(node, end=' ') # 노드 방문 처리 # 인접 노드 중 방문하지 않은 노드들을 큐에 추가 for neighbor in graph[node]: if neighbor not in visited: queue.append(neighbor) visited.add(neighbor) # 그래프 예시 (인접 리스트 형태) graph = { 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E'] } print("BFS 탐색 순서:") bfs(graph, 'A') # 출력: A B C D E F레벨 순서 트리 순회: 트리의 각 레벨을 순차적으로 방문
최단 경로 알고리즘: 그래프에서 두 노드 간의 최단 경로를 찾는 알고리즘(BFS 기반)
그 외 응용 분야
- 캐시 관리: LRU(Least Recently Used) 캐시 구현
- 작업 스케줄링: 작업을 순서대로 처리하기 위한 작업 큐
- 이벤트 처리: GUI 애플리케이션에서 사용자 이벤트를 처리하기 위한 이벤트 큐
- 웹 크롤링: 방문할 URL을 관리하기 위한 URL 큐
큐 구현 시 고려사항
큐를 구현할 때 고려해야 할 몇 가지 중요한 사항들이 있다:
메모리 효율성
- 고정 크기 vs 동적 크기: 용도에 맞게 적절한 구현 방식 선택
- 원형 큐 사용: 배열 기반 구현에서 메모리 낭비 방지
- 참조 제거: 객체를 dequeue한 후 참조를 명시적으로 제거하여 메모리 누수 방지
성능 최적화
- 연결 리스트 vs 배열: 연산 패턴에 따라 적절한 자료구조 선택
- 캐시 효율성: 배열은 연속 메모리를 사용하여 캐시 지역성이 좋음
- Lock-free 구현: 멀티스레드 환경에서 병목 현상 감소
스레드 안전성
멀티스레드 환경에서 큐를 사용할 때는 동시성 문제를 고려해야 한다:- 뮤텍스/세마포어: 큐 접근을 동기화
- 원자적 연산: CAS(Compare-And-Swap) 등의 원자적 연산 활용
- 블로킹 큐: 큐가 비어있을 때 dequeue를 호출한 스레드 블로킹
| |
효율적인 큐 구현 기법
양방향 큐 구현 최적화
덱(Deque)을 효율적으로 구현하기 위해서는 이중 연결 리스트를 사용하는 것이 좋다.
이렇게 하면 양쪽 끝에서의 삽입과 삭제가 모두 O(1) 시간에 수행된다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86# Python으로 구현한 이중 연결 리스트 기반 덱 class Node: def __init__(self, data): self.data = data self.prev = None self.next = None class DoublyLinkedListDeque: def __init__(self): self.head = None # 앞쪽 (front) self.tail = None # 뒤쪽 (rear) self.size_count = 0 def is_empty(self): return self.head is None def add_front(self, item): new_node = Node(item) if self.is_empty(): self.head = new_node self.tail = new_node else: new_node.next = self.head self.head.prev = new_node self.head = new_node self.size_count += 1 def add_rear(self, item): new_node = Node(item) if self.is_empty(): self.head = new_node self.tail = new_node else: self.tail.next = new_node new_node.prev = self.tail self.tail = new_node self.size_count += 1 def remove_front(self): if self.is_empty(): raise Exception("덱이 비어있습니다") item = self.head.data if self.head == self.tail: # 요소가 하나뿐인 경우 self.head = None self.tail = None else: self.head = self.head.next self.head.prev = None self.size_count -= 1 return item def remove_rear(self): if self.is_empty(): raise Exception("덱이 비어있습니다") item = self.tail.data if self.head == self.tail: # 요소가 하나뿐인 경우 self.head = None self.tail = None else: self.tail = self.tail.prev self.tail.next = None self.size_count -= 1 return item def peek_front(self): if self.is_empty(): raise Exception("덱이 비어있습니다") return self.head.data def peek_rear(self): if self.is_empty(): raise Exception("덱이 비어있습니다") return self.tail.data def size(self): return self.size_count배치 처리 기법
큐 연산을 최적화하기 위해 배치 처리(batch processing)를 적용할 수 있다. 여러 항목을 한 번에 처리함으로써 오버헤드를 줄일 수 있다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34# 배치 처리를 지원하는 큐 class BatchQueue: def __init__(self): self.items = [] def is_empty(self): return len(self.items) == 0 def enqueue(self, item): self.items.append(item) def enqueue_batch(self, items): self.items.extend(items) # 여러 항목을 한 번에 추가 def dequeue(self): if self.is_empty(): raise Exception("큐 언더플로우") return self.items.pop(0) def dequeue_batch(self, n): if len(self.items) < n: raise Exception("요청한 배치 크기가 큐의 크기보다 큽니다") batch = self.items[:n] self.items = self.items[n:] return batch def peek(self): if self.is_empty(): raise Exception("큐가 비어있습니다") return self.items[0] def size(self): return len(self.items)분산 큐 시스템
대규모 시스템에서는 큐를 여러 노드에 분산시켜 부하를 분산시키고 처리량을 높일 수 있다. 이러한 분산 큐 시스템의 예로는 Apache Kafka, RabbitMQ, Amazon SQS 등이 있다.분산 큐의 주요 특징:
- 확장성: 노드 추가를 통한 수평적 확장 가능
- 내결함성: 일부 노드 장애에도 서비스 지속
- 고가용성: 중단 없는 서비스 제공
- 메시지 지속성: 시스템 재시작 후에도 메시지 보존
고급 큐 활용 패턴
프로듀서-컨슈머 패턴
프로듀서-컨슈머 패턴은 데이터를 생산하는 프로세스(프로듀서)와 데이터를 소비하는 프로세스(컨슈머)가 큐를 통해 통신하는 패턴이다.이 패턴은 다음과 같은 상황에서 유용하다:
- 비동기 처리: 생산과 소비의 속도 차이 완화
- 작업 분배: 부하 분산을 통한 효율적인 작업 처리
- 병렬 처리: 여러 컨슈머가 동시에 작업 처리
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58# 간단한 프로듀서-컨슈머 패턴 구현 import threading import queue import random import time # 공유 큐 생성 buffer = queue.Queue(maxsize=10) # 최대 크기가 10인 블로킹 큐 # 프로듀서 함수 def producer(name, buffer): for i in range(10): item = f"{name}-{i}" buffer.put(item) # 큐가 가득 차면 블로킹 print(f"프로듀서 {name} 생산: {item}") time.sleep(random.random()) # 랜덤 지연 # 컨슈머 함수 def consumer(name, buffer): while True: try: item = buffer.get(block=True, timeout=1) # 최대 1초 대기 print(f"컨슈머 {name} 소비: {item}") buffer.task_done() time.sleep(random.random() * 2) # 랜덤 지연 except queue.Empty: # 타임아웃 발생 시 종료 조건 확인 if buffer.empty() and all_producers_done: break # 스레드 생성 및 실행 producers = [] all_producers_done = False for i in range(2): # 2개의 프로듀서 t = threading.Thread(target=producer, args=(f"P{i}", buffer)) producers.append(t) t.start() consumers = [] for i in range(3): # 3개의 컨슈머 t = threading.Thread(target=consumer, args=(f"C{i}", buffer)) consumers.append(t) t.start() # 모든 프로듀서 종료 대기 for t in producers: t.join() all_producers_done = True # 모든 프로듀서가 작업을 완료했음을 표시 # 모든 컨슈머 종료 대기 for t in consumers: t.join() # 모든 작업이 처리되었는지 확인 buffer.join() print("모든 작업 완료")백 프레셔(Back Pressure) 처리
백 프레셔는 소비자가 처리할 수 있는 속도보다 생산자가 더 빠르게 데이터를 생성할 때 발생하는 문제를 해결하기 위한 메커니즘이다.백 프레셔 처리 전략:
- 블로킹: 큐가 가득 차면 생산자 블로킹
- 드롭핑: 큐가 가득 차면 새 항목 버리기
- 스로틀링: 생산자의 생산 속도 제한
- 확장: 큐 용량 동적 증가 또는 컨슈머 추가
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30# 백 프레셔를 구현한 큐 class BackPressureQueue: def __init__(self, capacity): self.queue = queue.Queue(maxsize=capacity) self.capacity = capacity def enqueue(self, item, timeout=None): try: # 큐가 가득 차면 지정된 시간 동안 블로킹 self.queue.put(item, block=True, timeout=timeout) return True except queue.Full: # 타임아웃 발생 시 실패 처리 print("큐가 가득 찼습니다. 백 프레셔 발생") return False def dequeue(self): try: return self.queue.get(block=False) except queue.Empty: return None def size(self): return self.queue.qsize() def is_full(self): return self.queue.full() def is_empty(self): return self.queue.empty()실시간 데이터 처리
큐는 스트리밍 데이터나 이벤트 처리와 같은 실시간 시스템에 중요한 역할을 한다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28# 간단한 이벤트 처리 시스템 class Event: def __init__(self, event_type, data): self.event_type = event_type self.data = data self.timestamp = time.time() class EventQueue: def __init__(self): self.queue = queue.PriorityQueue() # 우선순위 큐 사용 def push_event(self, event, priority=0): # 낮은 숫자가 높은 우선순위 self.queue.put((priority, event)) def process_events(self, handlers): while not self.queue.empty(): priority, event = self.queue.get() # 이벤트 유형에 맞는 핸들러 찾기 if event.event_type in handlers: handler = handlers[event.event_type] try: handler(event) except Exception as e: print(f"이벤트 처리 중 오류 발생: {e}") else: print(f"처리할 수 없는 이벤트 유형: {event.event_type}")
큐 기반 알고리즘 사례 연구
레벨 순서 트리 순회(Level Order Traversal)
큐를 사용하여 트리를 레벨 단위로 순회하는 알고리즘.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49# 이진 트리 노드 class TreeNode: def __init__(self, val=0, left=None, right=None): self.val = val self.left = left self.right = right # 레벨 순서 순회 def level_order_traversal(root): if not root: return [] result = [] queue = [root] # 큐 초기화 (리스트로 간단히 구현) while queue: level_size = len(queue) # 현재 레벨의 노드 수 current_level = [] for _ in range(level_size): node = queue.pop(0) # 큐에서 노드 제거 current_level.append(node.val) # 현재 레벨에 노드 값 추가 # 자식 노드를 큐에 추가 if node.left: queue.append(node.left) if node.right: queue.append(node.right) result.append(current_level) # 현재 레벨 결과에 추가 return result # 예제 트리 생성: # 1 # / \ # 2 3 # / \ \ # 4 5 6 root = TreeNode(1) root.left = TreeNode(2) root.right = TreeNode(3) root.left.left = TreeNode(4) root.left.right = TreeNode(5) root.right.right = TreeNode(6) # 레벨 순서 순회 실행 print(level_order_traversal(root)) # 출력: [[1], [2, 3], [4, 5, 6]]위상 정렬(Topological Sort)
큐를 사용하여 방향 그래프의 노드를 의존성에 따라 정렬하는 알고리즘이다.
특히 선행 조건이 있는 작업 스케줄링에 유용하다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41# 큐를 이용한 위상 정렬 from collections import defaultdict, deque def topological_sort(vertices, edges): # 그래프 생성 graph = defaultdict(list) in_degree = {v: 0 for v in vertices} # 진입 차수 초기화 # 간선 정보 처리 for u, v in edges: graph[u].append(v) in_degree[v] += 1 # 진입 차수가 0인 노드를 큐에 추가 queue = deque([v for v in vertices if in_degree[v] == 0]) result = [] # 큐가 빌 때까지 반복 while queue: u = queue.popleft() result.append(u) # 인접 노드의 진입 차수 감소 for v in graph[u]: in_degree[v] -= 1 # 진입 차수가 0이 되면 큐에 추가 if in_degree[v] == 0: queue.append(v) # 모든 노드를 방문하지 못했다면 사이클이 존재 if len(result) != len(vertices): return "그래프에 사이클이 존재합니다" return result # 예제 vertices = ['A', 'B', 'C', 'D', 'E', 'F'] edges = [('A', 'B'), ('A', 'C'), ('B', 'D'), ('C', 'D'), ('D', 'E'), ('E', 'F')] print(topological_sort(vertices, edges)) # 출력: ['A', 'B', 'C', 'D', 'E', 'F']최단 경로 찾기(Shortest Path)
너비 우선 탐색(BFS)과 큐를 사용하여 비가중치 그래프에서 두 노드 간의 최단 경로를 찾는 알고리즘이다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35# 큐를 이용한 최단 경로 찾기 from collections import deque def shortest_path(graph, start, end): # 방문 여부 및 거리 추적 visited = set([start]) queue = deque([(start, [start])]) # (노드, 경로) 튜플 while queue: node, path = queue.popleft() # 목표 노드에 도달했는지 확인 if node == end: return path # 인접 노드 탐색 for neighbor in graph[node]: if neighbor not in visited: visited.add(neighbor) queue.append((neighbor, path + [neighbor])) return None # 경로가 없는 경우 # 예제 그래프 graph = { 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E'] } print(shortest_path(graph, 'A', 'F')) # 출력: ['A', 'C', 'F']슬라이딩 윈도우 최댓값
덱(Deque)을 사용하여 슬라이딩 윈도우 내의 최댓값을 효율적으로 찾는 알고리즘이다.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29# 덱을 이용한 슬라이딩 윈도우 최댓값 from collections import deque def max_sliding_window(nums, k): result = [] window = deque() # 인덱스를 저장하는 덱 for i, num in enumerate(nums): # 윈도우 범위를 벗어난 인덱스 제거 while window and window[0] < i - k + 1: window.popleft() # 현재 원소보다 작은 원소의 인덱스 제거 while window and nums[window[-1]] < num: window.pop() window.append(i) # 첫 번째 윈도우가 완성된 후부터 결과 수집 if i >= k - 1: result.append(nums[window[0]]) return result # 예제 nums = [1, 3, -1, -3, 5, 3, 6, 7] k = 3 print(max_sliding_window(nums, k)) # 출력: [3, 3, 5, 5, 6, 7]