동적 배열 (Dynamic Array)

동적 배열은 크기가 고정되지 않고 필요에 따라 자동으로 확장 또는 축소될 수 있는 데이터 구조이다.
정적 배열이 생성 시점에 고정된 크기를 가지는 반면, 동적 배열은 요소가 추가되거나 제거됨에 따라 내부적으로 메모리를 재할당하여 크기를 조정한다.

일반적인 프로그래밍 언어에서는 다음과 같이 구현되어 있다:

Python의 list
Java의 ArrayList
C++의 vector
JavaScript의 Array
기본적으로 동적 배열은 내부적으로 정적 배열을 사용하지만, 그 크기를 자동으로 관리하는 추상화 계층을 제공한다.

동적 배열은 단순하면서도 강력한 자료구조로, 현대 소프트웨어 개발에서 가장 기본적이고 널리 사용되는 데이터 구조 중 하나이다. 그 구현 원리와 성능 특성을 이해하면 다양한 문제 상황에서 적절한 자료구조를 선택하는 데 도움이 된다.

접근 패턴과 데이터 조작 요구사항에 따라 동적 배열이나 다른 데이터 구조(연결 리스트, 해시 테이블 등) 중 어떤 것이 최적인지 결정할 수 있다. 또한 동적 배열의 변형들은 특정 사용 사례에 맞게 최적화되어 있으므로, 문제 영역에 맞는 구현을 선택하는 것이 중요하다.

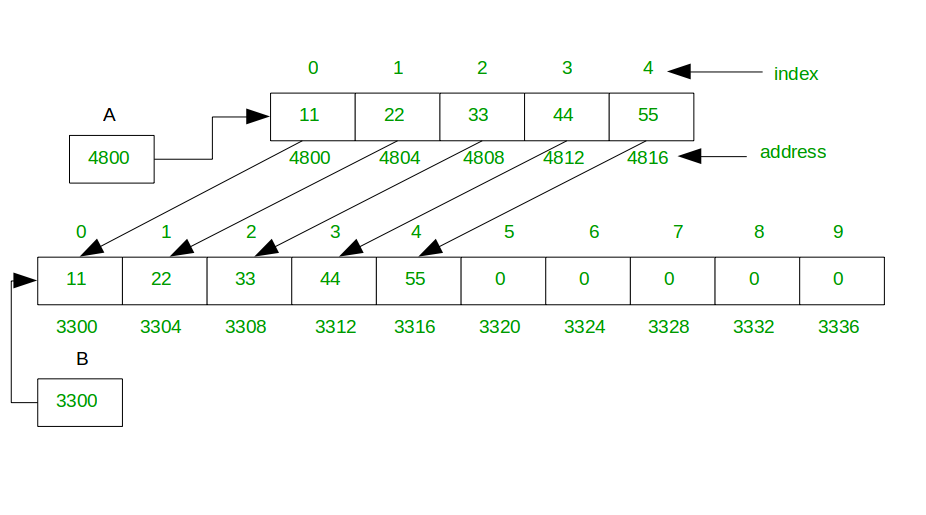
Dynamic Array — https://www.geeksforgeeks.org/how-do-dynamic-arrays-work/

동적 배열의 동작 원리

메모리 할당 전략

동적 배열의 핵심 메커니즘은 다음과 같다:

초기 할당: 처음 동적 배열을 생성할 때 특정 크기(예: 10개 요소)의 메모리 공간이 할당된다.
확장 메커니즘:
- 배열이 가득 차면(현재 용량에 도달하면), 더 큰 배열을 새로 할당한다.
- 일반적으로 기존 용량의 2배 크기로 확장한다(성장 계수 2).
- 기존 배열의 모든 요소를 새 배열로 복사한다.
- 기존 배열을 해제하고 새 배열로 참조를 업데이트한다.
축소 메커니즘:
- 일부 구현에서는 배열의 사용률이 낮아지면(예: 25% 미만) 크기를 줄이기도 한다.
- 필요한 크기보다 약간 큰 새 배열을 할당한다.
- 남아있는 요소들을 새 배열로 복사한다.

다음은 확장이 어떻게 작동하는지 보여주는 간단한 시각화:

1
2
3
4
5
6
7
8
초기 상태 (용량 4): [10, 20, 30, 40]
                     ↑  ↑  ↑  ↑
                     0  1  2  3

새 요소 추가 시 확장:
새 배열 (용량 8): [10, 20, 30, 40, 50, _, _, _]
                   ↑  ↑  ↑  ↑  ↑
                   0  1  2  3  4

시간 복잡도 분석

동적 배열 연산의 시간 복잡도는 다음과 같다:

접근(Access): O(1) - 인덱스를 통한 직접 접근
검색(Search): O(n) - 정렬되지 않은 경우
삽입(Insertion):
- 배열 끝에 추가: 평균 O(1) (분할 상환 분석)
- 최악의 경우(확장 필요): O(n)
- 임의 위치에 삽입: O(n)
삭제(Deletion):
- 배열 끝에서 제거: O(1)
- 임의 위치에서 제거: O(n)

분할 상환 분석

동적 배열의 특징 중 하나는 대부분의 삽입 연산이 O(1) 시간에 이루어지지만, 용량 확장 시점에는 O(n) 시간이 필요하다는 것이다.
이 때 **분할 상환 분석(amortized analysis)**을 사용하면 연산의 평균 성능을 더 정확히 파악할 수 있다.

n개의 요소를 순차적으로 삽입할 때:

대부분의 삽입은 O(1) 시간이 소요된다.
확장은 용량이 2배가 될 때마다 발생하므로, 1, 2, 4, 8, 16, … 번째 삽입에서 일어난다.
n번의 삽입에 필요한 총 연산은 약 3n에 가까워진다.
따라서 삽입의 분할 상환 시간 복잡도는 O(3n/n) = O(1)이다.

분할 상환 분석은 여러 연산이 수행되는 동안 발생하는 비용을 평균적으로 나누어 계산하는 방법. 이는 최악의 경우만 고려하는 Big-O 표기법과 달리, 연산이 반복될 때 평균적인 시간 복잡도를 계산하여 더 현실적인 비용을 제공한다.
동적 배열에서 추가 연산
동적 배열에서 데이터를 추가할 때 두 가지 주요 상황이 발생한다:
배열에 여유 공간이 있는 경우 - 새로운 데이터를 빈 인덱스에 저장한다.
시간 복잡도: O(1)
배열에 여유 공간이 없는 경우 (배열 크기 초과)
- 더 큰 배열을 생성하고 기존 데이터를 새 배열로 복사한 뒤 새로운 데이터를 추가한다. - 시간 복잡도: O(n) (n은 기존 배열의 크기)
분할 상환 분석 적용
새로운 데이터를 추가하는 과정 - 배열이 꽉 찼을 때, 새로운 배열을 할당하고 기존 데이터를 모두 복사해야 한다. - 일반적으로 동적 배열은 크기를 두 배로 늘린다(더블링 전략). 따라서, 새 배열 할당과 데이터 복사는 다음과 같이 진행된다:
| 추가 연산 | 배열 크기 | 데이터 복사 비용 |
| ——– | —– | ——— |
| 1번째 추가 | 1 | 0 |
| 2번째 추가 | 2 | 1 |
| 34번째 추가 | 4 | 2 |
| 58번째 추가 | 8 | 4 |
|… |… |… |
복사 비용은 1+2+4+⋯+n/2로 표현되며, 이는 등비수열의 합으로 계산된다:>
총 복사 비용=n−1
n번의 추가 연산 총 비용
빈 인덱스에 데이터를 저장하는 비용: O(n) (n번의 추가 연산)
데이터 복사 비용: O(n) (최대 n−1)
따라서, 총 비용은 O(2n), 즉 O(n)이다.

동적 배열의 장단점

장점

유연한 크기: 필요에 따라 자동으로 크기가 조정되어 메모리 관리가 편리하다.
상수 시간 접근: 인덱스를 통한 O(1) 시간 접근이 가능하다.
효율적인 끝단 연산: 배열 끝에 요소를 추가하거나 제거하는 작업이 평균적으로 O(1) 시간에 이루어진다.
캐시 지역성: 메모리에 연속적으로 저장되어 캐시 효율성이 높다.

단점

확장 비용: 용량 확장 시 모든 요소를 복사해야 하므로 일시적으로 O(n) 시간이 소요된다.
메모리 오버헤드: 항상 실제 사용량보다 많은 공간을 할당하므로 일부 메모리가 낭비될 수 있다.
중간 삽입/삭제 비효율: 배열 중간에 요소를 삽입하거나 삭제할 때 O(n) 시간이 필요하다.
요소 이동: 삽입/삭제 시 요소들을 이동시켜야 하는 오버헤드가 있다.

동적 배열 구현

Python으로 간단한 동적 배열 클래스를 구현:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
class DynamicArray:
    def __init__(self, capacity=10):
        # 내부적으로 고정 크기 배열 사용
        self.capacity = capacity  # 현재 할당된 공간
        self.length = 0  # 실제 저장된 요소 수
        self.array = [None] * capacity  # 내부 배열
    
    def __len__(self):
        return self.length
    
    def __getitem__(self, index):
        if not 0 <= index < self.length:
            raise IndexError('인덱스 범위 초과')
        return self.array[index]
    
    def append(self, item):
        # 용량이 꽉 찼으면 확장
        if self.length == self.capacity:
            self._resize(2 * self.capacity)
        
        # 새 요소 추가
        self.array[self.length] = item
        self.length += 1
    
    def pop(self):
        if self.length == 0:
            raise IndexError('빈 배열')
        
        # 마지막 요소 제거
        self.length -= 1
        item = self.array[self.length]
        self.array[self.length] = None
        
        # 사용 중인 공간이 용량의 1/4 이하면 축소
        if self.length > 0 and self.length <= self.capacity // 4:
            self._resize(self.capacity // 2)
            
        return item
    
    def insert(self, index, item):
        if not 0 <= index <= self.length:
            raise IndexError('인덱스 범위 초과')
        
        # 용량이 꽉 찼으면 확장
        if self.length == self.capacity:
            self._resize(2 * self.capacity)
        
        # 삽입 위치 이후의 요소들을 한 칸씩 뒤로 이동
        for i in range(self.length, index, -1):
            self.array[i] = self.array[i-1]
        
        # 새 요소 삽입
        self.array[index] = item
        self.length += 1
    
    def remove(self, index):
        if not 0 <= index < self.length:
            raise IndexError('인덱스 범위 초과')
        
        # 제거할 요소 저장
        item = self.array[index]
        
        # 제거할 요소 이후의 요소들을 한 칸씩 앞으로 이동
        for i in range(index, self.length - 1):
            self.array[i] = self.array[i+1]
        
        # 마지막 요소 None으로 설정
        self.array[self.length - 1] = None
        self.length -= 1
        
        # 사용 중인 공간이 용량의 1/4 이하면 축소
        if self.length > 0 and self.length <= self.capacity // 4:
            self._resize(self.capacity // 2)
            
        return item
    
    def _resize(self, new_capacity):
        # 새로운 배열 생성
        new_array = [None] * new_capacity
        
        # 기존 요소 복사
        for i in range(self.length):
            new_array[i] = self.array[i]
        
        # 배열 참조 업데이트
        self.array = new_array
        self.capacity = new_capacity

동적 배열 최적화 기법

성장 계수 조정
일반적으로 동적 배열은 용량을 2배씩 증가시키지만, 다양한 성장 계수가 사용될 수 있다:
- 계수 2: 가장 일반적인 선택으로, 균형 잡힌 성능 제공
- 계수 1.5: C++의 일부 vector 구현에서 사용, 메모리 효율성 향상
- 계수 √2: 일부 특수 구현에서 사용, 메모리 사용량과 복사 비용의 균형
지연 초기화
큰 배열이 필요할 수 있지만 초기에는 적은 요소만 사용하는 경우, 지연 초기화 기법을 사용하여 실제 필요할 때까지 메모리 할당을 미룰 수 있다.
캐시 최적화
메모리 접근 패턴을 최적화하여 캐시 효율성을 높일 수 있다:
- 요소 크기를 캐시 라인 크기에 맞추기
- 관련 데이터를 함께 저장하여 지역성 향상
- 메모리 정렬 고려

동적 배열의 실제 응용

동적 배열은 다양한 소프트웨어 시스템에서 광범위하게 사용된다:

데이터베이스 시스템: 레코드 저장 및 관리
텍스트 편집기: 문자 및 줄 관리
이미지 처리: 픽셀 데이터 저장
웹 브라우저: DOM 요소 관리
게임 개발: 게임 객체 관리
다양한 알고리즘 구현: 정렬, 검색, 그래프 알고리즘 등

고급 동적 배열 변형

갭 버퍼 (Gap Buffer)
텍스트 편집기에서 자주 사용되는 갭 버퍼는 동적 배열의 변형으로, 현재 커서 위치에 빈 공간(갭)을 유지하여 삽입과 삭제를 효율적으로 처리gksek.

1
2
3
텍스트: "Hello World"
갭 버퍼 (커서가 'o'와 ' ' 사이): [H, e, l, l, o, _, _, _, _, _,  , W, o, r, l, d]
                                             ↑ 갭 ↑

원형 버퍼 (Circular Buffer)
동적 배열의 또 다른 변형인 원형 버퍼는 시작과 끝 위치를 포인터로 관리하여 FIFO(선입선출) 연산을 효율적으로 지원gksek. 스트리밍 데이터 처리나 큐 구현에 자주 사용된다.
분할 배열 (Segmented Array)
매우 큰 동적 배열을 관리할 때 사용되는 분할 배열은 여러 개의 작은 배열 세그먼트를 트리 구조로 조직하여 메모리 재할당 비용을 줄인다. 이는 B-트리와 유사한 접근 방식을 사용한다.

현대 프로그래밍 언어에서의 구현

Python의 List
Python의 list는 동적 배열을 구현한 자료구조:
- 내부적으로 C 배열 사용
- 용량을 0, 4, 8, 16, … 등으로 증가시키며, 작은 크기에서는 다른 성장 패턴 사용
- 일반적으로 현재 크기보다 1/8 이상 여유 공간을 유지
Java의 ArrayList
Java의 ArrayList는 다음과 같은 특징을 가진 동적 배열:
- 기본 용량은 10
- 용량이 부족할 때 크기를 1.5배로 증가
- 크기 축소는 자동으로 이루어지지 않음
C++의 Vector
C++의 std::vector는 다음과 같은 특징을 가진다:
- 구현에 따라 다르지만 일반적으로 2배 또는 1.5배 성장 계수 사용
- 명시적인 shrink_to_fit() 메서드로 크기 축소 가능
- 메모리 할당기(allocator) 커스터마이징 지원