선택 정렬 (Selection Sort)

선택 정렬은 가장 직관적이고 이해하기 쉬운 정렬 알고리즘 중 하나이다.

선택 정렬은 개념적으로 가장 단순한 정렬 알고리즘 중 하나로, 알고리즘을 처음 배우는 사람들에게 좋은 시작점이 된다. 비록 대규모 데이터에서는 효율적이지 않지만, 특정 상황에서는 실용적인 선택이 될 수 있다.

선택 정렬의 핵심 특징은 다음과 같다:

구현이 매우 간단합니다.
교환 연산의 수가 적습니다(최대 n-1번).
메모리 사용이 최소화된다.
입력 데이터의 상태와 관계없이 일정한 성능을 보인다.

더 효율적인 정렬 알고리즘이 많이 존재하지만, 선택 정렬은 그 단순함과 직관적인 접근 방식으로 알고리즘 학습에 중요한 역할을 한다. 또한 작은 데이터셋이나 특정 제약 조건이 있는 환경에서는 여전히 유용한 알고리즘이다.

Selection Sort — https://www.perplexity.ai/search/computer-architecture-eseo-cac-DTWMIKIVRnOtdnLMm0Ydrw

선택 정렬의 기본 원리

선택 정렬은 다음과 같은 간단한 아이디어에 기반한다:

정렬되지 않은 부분에서 최솟값(또는 최댓값)을 찾는다.
이 값을 정렬되지 않은 부분의 첫 번째 요소와 교환한다.
정렬된 부분의 경계를 한 칸 오른쪽으로 이동시킨다.
배열 전체가 정렬될 때까지 위 과정을 반복한다.

이 과정을 거치면 배열의 왼쪽부터 차례대로 정렬된 요소들이 쌓이게 된다.

선택 정렬의 시각화 과정

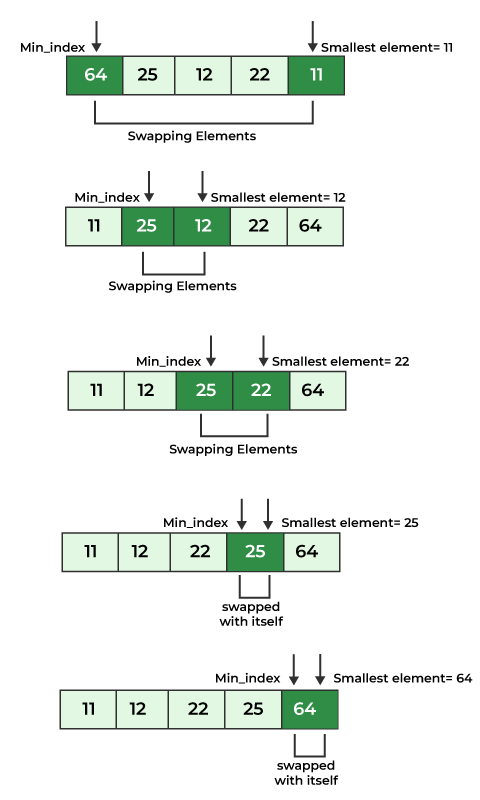
[64, 25, 12, 22, 11] 배열을 선택 정렬로 정렬하는 과정을 단계별로 시각화:

전체 배열에서 최솟값 11을 찾아 첫 번째 위치(인덱스 0)와 교환

1
2
3
4
[64, 25, 12, 22, 11] → [11, 25, 12, 22, 64]
  ^               ^      ^-----------------> 정렬된 부분
  |               |
  +---------------+ 교환

나머지 배열 [25, 12, 22, 64]에서 최솟값 12를 찾아 두 번째 위치(인덱스 1)와 교환

1
2
3
4
[11, 25, 12, 22, 64] → [11, 12, 25, 22, 64]
      ^   ^                ^-------------> 정렬된 부분
      |   |
      +---+ 교환

나머지 배열 [25, 22, 64]에서 최솟값 22를 찾아 세 번째 위치(인덱스 2)와 교환

1
2
3
4
[11, 12, 25, 22, 64] → [11, 12, 22, 25, 64]
          ^   ^            ^----------> 정렬된 부분
          |   |
          +---+ 교환

나머지 배열 [25, 64]에서 최솟값 25는 이미 네 번째 위치(인덱스 3)에 있으므로 교환 필요 없음

1
2
3
4
[11, 12, 22, 25, 64] → [11, 12, 22, 25, 64]
              ^                ^-------> 정렬된 부분
              |
              + 이미 최솟값

마지막 요소 64는 이미 올바른 위치에 있으므로 정렬 완료

1
2
3
[11, 12, 22, 25, 64]
                  ^
                  + 정렬 완료

이렇게 매 단계마다 정렬되지 않은 부분에서 최솟값을 찾아 정렬된 부분의 끝에 추가하는 방식으로 정렬이 진행된다.

선택 정렬의 구현

아래는 Python으로 구현한 선택 정렬 알고리즘:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def selection_sort(arr):
    n = len(arr)
    
    # 배열의 각 위치에 대해 반복
    for i in range(n):
        # 현재 위치를 최솟값의 인덱스로 초기화
        min_idx = i
        
        # i부터 끝까지 탐색하여 최솟값 찾기
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
                
        # 찾은 최솟값을 현재 위치와 교환
        arr[i], arr[min_idx] = arr[min_idx], arr[i]
    
    return arr

# 사용 예시
arr = [64, 25, 12, 22, 11]
sorted_arr = selection_sort(arr)
print(sorted_arr)  # [11, 12, 22, 25, 64]

이 코드는 모든 단계에서 배열의 일부분에서 최솟값을 찾아 적절한 위치로 이동시키는 과정을 명확히 보여준다.

선택 정렬의 특징

시간 복잡도
- 최선의 경우: O(n²) - 이미 정렬되어 있는 경우에도 모든 요소를 비교
- 평균적인 경우: O(n²)
- 최악의 경우: O(n²)
  선택 정렬의 가장 큰 특징은 입력 배열의 상태와 관계없이 항상 동일한 시간 복잡도를 가진다. 이는 항상 모든 요소를 비교해야 하기 때문이다.
공간 복잡도
- O(1) - 추가 메모리가 거의 필요 없는 제자리(in-place) 정렬 알고리즘
안정성
- 선택 정렬은 기본적으로 불안정(unstable) 정렬이다. 같은 값을 가진 요소들의 상대적 순서가 정렬 과정에서 바뀔 수 있다.
  예를 들어, [4, 2, 3, 4', 1]이라는 배열이 있다고 가정해 보면(4’는 첫 번째 4와 구분하기 위한 표시). 선택 정렬 후에는 [1, 2, 3, 4', 4] 또는 [1, 2, 3, 4, 4']와 같이 두 개의 4의 순서가 바뀔 수 있다.

선택 정렬의 성능 개선 방법

양방향 선택 정렬(Bidirectional Selection Sort)
한 번의 반복에서 최솟값과 최댓값을 동시에 찾아 양쪽 끝에 배치하는 방식:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def bidirectional_selection_sort(arr):
    n = len(arr)
    left, right = 0, n - 1

    while left < right:
        min_idx = left
        max_idx = left

        # 현재 범위에서 최솟값과 최댓값 찾기
        for i in range(left, right + 1):
            if arr[i] < arr[min_idx]:
                min_idx = i
            elif arr[i] > arr[max_idx]:
                max_idx = i

        # 최솟값을 왼쪽 끝으로 이동
        if min_idx != left:
            arr[left], arr[min_idx] = arr[min_idx], arr[left]

            # 만약 최댓값이 최솟값의 위치에 있었다면 인덱스 조정
            if max_idx == left:
                max_idx = min_idx

        # 최댓값을 오른쪽 끝으로 이동
        if max_idx != right:
            arr[right], arr[max_idx] = arr[max_idx], arr[right]

        # 범위 좁히기
        left += 1
        right -= 1

    return arr

이 방식은 비교 횟수는 동일하지만, 교환 횟수를 줄여 약간의 성능 향상을 기대할 수 있다.

힙 정렬(Heap Sort)로의 확장
선택 정렬의 아이디어를 확장하여 힙 자료구조를 활용하면 O(n log n)의 시간 복잡도를 가진 힙 정렬이 된다.
힙을 사용하면 최솟값(또는 최댓값)을 O(log n) 시간에 찾을 수 있어 전체 시간 복잡도가 개선된다.

6. 선택 정렬의 실제 적용

적합한 사용 상황
선택 정렬은 다음과 같은 상황에서 고려할 수 있다:
1. 간단한 구현이 필요할 때: 코드가 짧고 이해하기 쉬움
2. 작은 크기의 배열: 요소 수가 적은 배열에서는 준수한 성능
3. 교환 연산이 비싼 경우: 선택 정렬은 최대 n번의 교환만 수행
실제 사용 예시
- 교육용 목적: 알고리즘의 기본 개념 이해
- 임베디드 시스템: 메모리가 제한적인 환경
- 이미 거의 정렬된 배열에서 몇 개의 요소만 올바른 위치에 넣어야 할 때

실제 코드 분석 - 선택 정렬의 변형들

최솟값과 최댓값을 동시에 찾는 변형

이 변형은 각 반복에서 최솟값과 최댓값을 동시에 찾아 양쪽에서 정렬하는 방식으로, 비교 횟수를 줄일 수 있다:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def min_max_selection_sort(arr):
    n = len(arr)
    left = 0
    right = n - 1
    
    while left < right:
        # 최솟값과 최댓값의 초기 인덱스
        min_idx = left
        max_idx = left
        
        for i in range(left + 1, right + 1):
            if arr[i] < arr[min_idx]:
                min_idx = i
            elif arr[i] > arr[max_idx]:
                max_idx = i
        
        # 최솟값을 왼쪽에 배치
        arr[left], arr[min_idx] = arr[min_idx], arr[left]
        
        # 만약 최댓값이 최솟값 위치에 있었다면 인덱스 업데이트
        if max_idx == left:
            max_idx = min_idx
        
        # 최댓값을 오른쪽에 배치
        arr[right], arr[max_idx] = arr[max_idx], arr[right]
        
        # 포인터 이동
        left += 1
        right -= 1
    
    return arr

재귀적 구현

선택 정렬을 재귀적으로 구현할 수도 있다:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
def recursive_selection_sort(arr, start_idx=0):
    # 종료 조건
    if start_idx >= len(arr) - 1:
        return
    
    # 최솟값 찾기
    min_idx = start_idx
    for i in range(start_idx + 1, len(arr)):
        if arr[i] < arr[min_idx]:
            min_idx = i
    
    # 최솟값을 현재 위치와 교환
    if min_idx != start_idx:
        arr[start_idx], arr[min_idx] = arr[min_idx], arr[start_idx]
    
    # 다음 위치부터 재귀적으로 정렬
    recursive_selection_sort(arr, start_idx + 1)
    
    return arr