퀵 정렬 (Quick Sort)

퀵 정렬은 1960년 Tony Hoare가 개발한 효율적인 분할 정복(Divide and Conquer) 알고리즘으로, 평균적으로 매우 빠른 성능을 보이는 정렬 방식이다. 실제 많은 프로그래밍 언어의 표준 라이브러리에 구현되어 있을 정도로 실용적인 정렬 알고리즘이다.

퀵 정렬은 간단한 아이디어를 바탕으로 하면서도 매우 효율적인 정렬 알고리즘이다.
평균적인 성능이 우수하고 실제 구현에서 다양한 최적화 기법을 적용할 수 있어 많은 환경에서 선호된다.
최악의 경우를 대비한 피벗 선택 최적화와 하이브리드 접근 방식을 통해 단점을 보완하여 현대적인 정렬 알고리즘의 기반이 되고 있다.

퀵 정렬은 분할 정복 패러다임의 대표적인 예시로, 컴퓨터 과학 교육에서도 중요한 알고리즘으로 가르쳐지며, 그 원리와 최적화 방법은 다양한 문제 해결 방법에 응용될 수 있다.

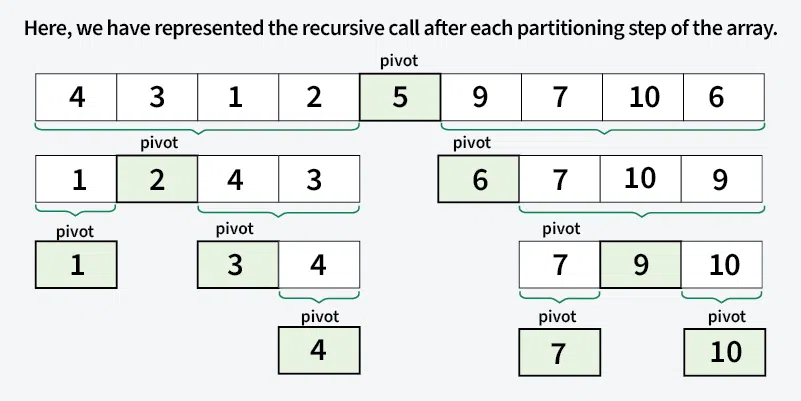
Quick Sort — https://www.geeksforgeeks.org/quick-sort-algorithm/

퀵 정렬의 기본 원리

퀵 정렬은 다음과 같은 핵심 단계로 동작한다:

피벗 선택(Pivot Selection): 배열에서 하나의 요소를 피벗으로 선택한다.
분할(Partitioning): 피벗을 기준으로 배열을 두 부분으로 나눈다. 피벗보다 작은 값들은 왼쪽, 큰 값들은 오른쪽으로 이동시킨다.
재귀(Recursion): 분할된 두 부분 배열에 대해 재귀적으로 퀵 정렬을 수행한다.
이 과정은 부분 배열의 크기가 1이 되거나 빈 배열이 될 때까지 계속된다.

퀵 정렬의 시각화 과정

[5, 3, 7, 2, 9, 1, 4] 배열을 퀵 정렬로 정렬하는 과정을 시각화:

첫 번째 단계: 피벗 = 5

1
2
3
4
초기 배열: [5, 3, 7, 2, 9, 1, 4]
피벗보다 작은 요소들: [3, 2, 1, 4]
피벗: [5]
피벗보다 큰 요소들: [7, 9]

두 번째 단계 (왼쪽 부분 배열): 피벗 = 3

1
2
3
4
현재 배열: [3, 2, 1, 4]
피벗보다 작은 요소들: [2, 1]
피벗: [3]
피벗보다 큰 요소들: [4]

세 번째 단계 (왼쪽의 왼쪽 부분 배열): 피벗 = 2

1
2
3
4
현재 배열: [2, 1]
피벗보다 작은 요소들: [1]
피벗: [2]
피벗보다 큰 요소들: []

네 번째 단계 (오른쪽 부분 배열): 피벗 = 7

1
2
3
4
현재 배열: [7, 9]
피벗보다 작은 요소들: []
피벗: [7]
피벗보다 큰 요소들: [9]

최종 결과:

1
2
3
[1] + [2] + [] = [1, 2]
[1, 2] + [3] + [4] = [1, 2, 3, 4]
[1, 2, 3, 4] + [5] + [7, 9] = [1, 2, 3, 4, 5, 7, 9]

퀵 정렬의 특징

시간 복잡도
- 최선의 경우: O(n log n) - 피벗이 항상 배열을 균등하게 분할할 때
- 평균적인 경우: O(n log n)
- 최악의 경우: O(n²) - 피벗이 항상 가장 작거나 가장 큰 요소일 때 (이미 정렬된 배열에서 첫 번째나 마지막 요소를 피벗으로 선택하는 경우)
공간 복잡도
- 기본 구현: O(n) - 재귀 호출로 인한 스택 공간
- 인플레이스 구현: O(log n) - 재귀 호출로 인한 스택 공간만 필요
안정성
- 퀵 정렬은 기본적으로 불안정(unstable) 정렬. 동일한 값을 가진 요소들의 상대적 순서가 정렬 후에 유지되지 않을 수 있다.

퀵 정렬의 장단점

장점

평균적으로 매우 빠른 정렬 속도 (실제로 가장 빠른 정렬 알고리즘 중 하나)
추가 메모리를 적게 사용하는 인플레이스 구현 가능
캐시 지역성이 좋아 실제 환경에서 우수한 성능

단점

최악의 경우 O(n²) 시간 복잡도
불안정 정렬
이미 정렬된 데이터에 대해 비효율적 (피벗 선택 최적화로 개선 가능)

퀵 정렬의 구현

다음은 Python으로 구현한 기본적인 퀵 정렬 알고리즘:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
def quick_sort(arr):
    # 종료 조건: 배열의 길이가 1 이하면 이미 정렬된 것으로 간주
    if len(arr) <= 1:
        return arr
    
    # 피벗 선택 (여기서는 첫 번째 요소를 선택)
    pivot = arr[0]
    
    # 분할: 피벗보다 작은 요소들
    left = [x for x in arr[1:] if x <= pivot]
    
    # 분할: 피벗보다 큰 요소들
    right = [x for x in arr[1:] if x > pivot]
    
    # 재귀적으로 정렬하고 결과 병합
    return quick_sort(left) + [pivot] + quick_sort(right)

# 사용 예시
arr = [10, 7, 8, 9, 1, 5]
sorted_arr = quick_sort(arr)
print(sorted_arr)  # [1, 5, 7, 8, 9, 10]

더 효율적인 구현을 위한 인플레이스(in-place) 방식의 퀵 정렬:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def quick_sort_inplace(arr, low, high):
    if low < high:
        # 파티션 인덱스 찾기
        pi = partition(arr, low, high)
        
        # 피벗 기준 왼쪽 부분 정렬
        quick_sort_inplace(arr, low, pi - 1)
        
        # 피벗 기준 오른쪽 부분 정렬
        quick_sort_inplace(arr, pi + 1, high)
    
    return arr

def partition(arr, low, high):
    # 피벗 (여기서는 맨 오른쪽 요소)
    pivot = arr[high]
    
    # 작은 요소들이 위치할 인덱스
    i = low - 1
    
    for j in range(low, high):
        # 현재 요소가 피벗보다 작거나 같으면
        if arr[j] <= pivot:
            # 작은 요소 인덱스 증가
            i += 1
            # 요소 교환
            arr[i], arr[j] = arr[j], arr[i]
    
    # 피벗을 정확한 위치로 이동
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    
    # 피벗의 위치 반환
    return i + 1

# 사용 예시
arr = [10, 7, 8, 9, 1, 5]
quick_sort_inplace(arr, 0, len(arr) - 1)
print(arr)  # [1, 5, 7, 8, 9, 10]

퀵 정렬의 최적화 방법

피벗 선택 최적화
피벗 선택은 퀵 정렬의 성능에 큰 영향을 미친다.
일반적인 피벗 선택 방법들:

첫 번째 또는 마지막 요소: 구현이 간단하지만, 정렬된 배열에서 최악의 성능
중간 요소: 첫 번째, 중간, 마지막 요소 중 중앙값(median)을 피벗으로 선택
무작위 요소: 랜덤하게 피벗 선택, 최악의 경우를 피할 확률 높음

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
def quick_sort_median_of_three(arr, low, high):
    if low < high:
        # 중앙값 피벗 선택
        mid = (low + high) // 2
        if arr[low] > arr[mid]:
            arr[low], arr[mid] = arr[mid], arr[low]
        if arr[low] > arr[high]:
            arr[low], arr[high] = arr[high], arr[low]
        if arr[mid] > arr[high]:
            arr[mid], arr[high] = arr[high], arr[mid]

        # 중간 값을 피벗으로 사용
        pivot = arr[mid]

        # 나머지 과정은 동일
        # …

작은 부분 배열에 대한 최적화
작은 크기의 부분 배열에 대해서는 삽입 정렬과 같은 더 효율적인 알고리즘을 사용할 수 있다:

1
2
3
4
5
6
7
8
def optimized_quick_sort(arr, low, high):
    # 작은 배열에 대해 삽입 정렬 사용
    if high - low <= 10:
        insertion_sort(arr, low, high)
        return

    # 이하 기존 퀵 정렬과 동일
    # …

꼬리 재귀 최적화
재귀 호출 대신 반복문을 사용하여 스택 오버플로를 방지하고 성능을 개선할 수 있다:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def quick_sort_tail_recursive(arr, low, high):
    while low < high:
        # 파티션 수행
        pi = partition(arr, low, high)

        # 더 작은 부분을 재귀적으로 처리
        if pi - low < high - pi:
            quick_sort_tail_recursive(arr, low, pi - 1)
            low = pi + 1
        else:
            quick_sort_tail_recursive(arr, pi + 1, high)
            high = pi - 1

퀵 정렬의 응용

퀵 선택(Quick Select)
퀵 정렬의 원리를 이용하여 배열에서 k번째로 작은 요소를 찾는 알고리즘이다. 평균 시간 복잡도는 O(n)이다:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def quick_select(arr, k):
    """배열에서 k번째로 작은 요소를 찾는 함수"""
    if not 1 <= k <= len(arr):
        return None

    def select(arr, left, right, k):
        if left == right:
            return arr[left]

        pivot_index = partition(arr, left, right)

        # 피벗의 위치가 찾는 k번째와 일치하면 반환
        if k == pivot_index + 1:
            return arr[pivot_index]
        # k가 피벗 위치보다 작으면 왼쪽 부분 배열 탐색
        elif k < pivot_index + 1:
            return select(arr, left, pivot_index - 1, k)
        # k가 피벗 위치보다 크면 오른쪽 부분 배열 탐색
        else:
            return select(arr, pivot_index + 1, right, k)

    return select(arr, 0, len(arr) - 1, k)

3-방향 퀵 정렬(3-Way Quick Sort)
중복 요소가 많은 배열에 대해 효율적인 퀵 정렬 변형:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def quick_sort_three_way(arr, low, high):
    if high <= low:
        return

    lt = low       # 피벗보다 작은 값 경계
    gt = high      # 피벗보다 큰 값 경계
    i = low + 1    # 현재 탐색 위치
    pivot = arr[low]

    while i <= gt:
        if arr[i] < pivot:
            arr[lt], arr[i] = arr[i], arr[lt]
            lt += 1
            i += 1
        elif arr[i] > pivot:
            arr[i], arr[gt] = arr[gt], arr[i]
            gt -= 1
        else:
            i += 1

    # 재귀적으로 정렬
    quick_sort_three_way(arr, low, lt - 1)
    quick_sort_three_way(arr, gt + 1, high)

퀵 정렬의 실제 구현 사례

C++ STL의 std::sort
C++의 표준 라이브러리에서 구현된 std::sort는 퀵 정렬, 삽입 정렬, 힙 정렬의 하이브리드 형태:
1. 기본적으로 인트로소트(Introsort, 퀵 정렬 기반)를 사용
2. 재귀 깊이가 일정 수준 이상 깊어지면 힙 정렬로 전환
3. 작은 부분 배열에는 삽입 정렬 적용
Java의 Arrays.sort()
Java의 기본 정렬 메서드도 유사한 하이브리드 접근 방식을 사용:
1. 기본 자료형의 경우 듀얼 피벗 퀵 정렬(Dual-Pivot Quicksort) 사용
2. 객체의 경우 안정성을 위해 TimSort(병합 정렬과 삽입 정렬의 하이브리드) 사용