병합 정렬 (Merge Sort)

병합 정렬 (Merge Sort)

병합 정렬은 분할 정복(Divide and Conquer) 패러다임을 기반으로 하는 효율적인 정렬 알고리즘이다.
여러 정렬 알고리즘 중에서도 안정적인 성능과 일관된 시간 복잡도를 제공하는 방식으로 널리 사용된다.

병합 정렬은 안정적인 성능과 예측 가능한 시간 복잡도를 제공하는 매우 유용한 정렬 알고리즘. 추가 메모리가 필요하다는 단점이 있지만, 대규모 데이터 처리나 외부 정렬에 적합하며, 안정적인 정렬이 필요한 상황에서 특히 유용하다.
알고리즘의 단순성과 병렬화 가능성도 중요한 장점이다.

병합 정렬의 기본 원리

병합 정렬은 다음 세 단계로 동작한다:

1. 분할(Divide): 입력 배열을 두 개의 부분 배열로 나눈다.
2. 정복(Conquer): 두 부분 배열을 재귀적으로 정렬한다.
3. 병합(Merge): 정렬된 두 부분 배열을 하나의 정렬된 배열로 병합한다.
   이 과정은 부분 배열의 크기가 1이 될 때까지 계속되며, 크기가 1인 배열은 이미 정렬되어 있다고 간주한다.

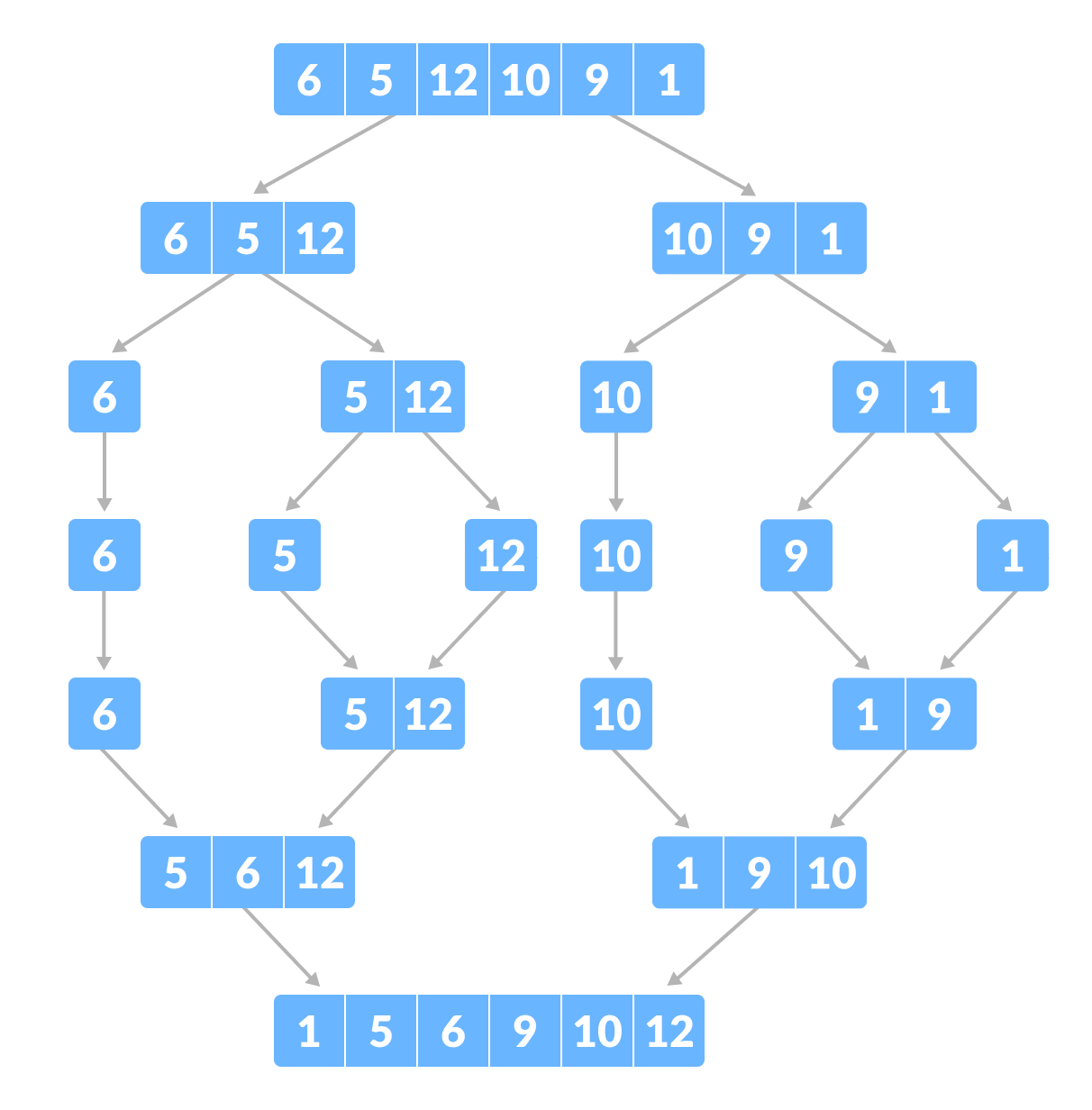
병합 정렬의 시각화 과정

[5, 2, 4, 7, 1, 3, 8, 6] 배열을 병합 정렬로 정렬하는 과정을 시각화:

분할 단계:

1
2
3
4
5
6
7

[5, 2, 4, 7, 1, 3, 8, 6]
          /        \
   [5, 2, 4, 7]    [1, 3, 8, 6]
     /    \          /    \
  [5, 2]  [4, 7]   [1, 3]  [8, 6]
   / \     / \      / \     / \
 [5] [2] [4] [7]  [1] [3] [8] [6]

병합 단계:

1
2
3
4
5
6
7

 [5] [2] [4] [7]  [1] [3] [8] [6]
   \ /     \ /      \ /     \ /
  [2, 5]  [4, 7]   [1, 3]  [6, 8]
     \    /          \    /
   [2, 4, 5, 7]    [1, 3, 6, 8]
          \        /
    [1, 2, 3, 4, 5, 6, 7, 8]

병합 정렬의 특징

1. 시간 복잡도

   • 최선의 경우: O(n log n)
   • 평균적인 경우: O(n log n)
   • 최악의 경우: O(n log n)
     병합 정렬은 입력 배열의 상태와 관계없이 항상 일정한 시간 복잡도를 보이는 것이 큰 장점이다.

2. 공간 복잡도

   • O(n) - 정렬 과정에서 추가적인 배열이 필요하다.

3. 안정성

   • 병합 정렬은 안정적인 정렬 알고리즘이다.
   • 동일한 값을 가진 요소들의 상대적인 순서가 정렬 후에도 유지된다.

병합 정렬의 구현

다음은 Python으로 구현한 병합 정렬 알고리즘:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

def merge_sort(arr):
    # 종료 조건: 배열의 길이가 1 이하면 이미 정렬된 것으로 간주
    if len(arr) <= 1:
        return arr
    
    # 분할 단계: 배열을 두 부분으로 나눔
    mid = len(arr) // 2
    left_half = arr[:mid]
    right_half = arr[mid:]
    
    # 정복 단계: 두 부분을 재귀적으로 정렬
    left_half = merge_sort(left_half)
    right_half = merge_sort(right_half)
    
    # 병합 단계: 정렬된 두 부분을 병합
    return merge(left_half, right_half)

def merge(left, right):
    result = []
    i = j = 0
    
    # 두 배열의 요소를 비교하여 작은 값부터 결과 배열에 추가
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    
    # 남은 요소들 추가
    result.extend(left[i:])
    result.extend(right[j:])
    
    return result

# 사용 예시
arr = [38, 27, 43, 3, 9, 82, 10]
sorted_arr = merge_sort(arr)
print(sorted_arr)  # [3, 9, 10, 27, 38, 43, 82]

입력 배열:

1

arr = [38, 27, 43, 3, 9, 82, 10]

실행 과정: merge_sort는 “분할(Divide) → 정복(Conquer) → 병합(Merge)” 단계를 거쳐 정렬된다.

1. 분할 (Divide) 배열을 절반으로 나누면서 재귀 호출이 계속된다.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

   merge_sort([38, 27, 43, 3, 9, 82, 10]) ├─ merge_sort([38, 27, 43]) │ ├─ merge_sort([38]) → [38] (Base Case) │ ├─ merge_sort([27, 43]) │ │ ├─ merge_sort([27]) → [27] (Base Case) │ │ ├─ merge_sort([43]) → [43] (Base Case) │ │ └─ merge([27], [43]) → [27, 43] │ └─ merge([38], [27, 43]) → [27, 38, 43] │ ├─ merge_sort([3, 9, 82, 10]) ├─ merge_sort([3, 9]) │ ├─ merge_sort([3]) → [3] (Base Case) │ ├─ merge_sort([9]) → [9] (Base Case) │ └─ merge([3], [9]) → [3, 9] │ ├─ merge_sort([82, 10]) │ ├─ merge_sort([82]) → [82] (Base Case) │ ├─ merge_sort([10]) → [10] (Base Case) │ └─ merge([82], [10]) → [10, 82] │ └─ merge([3, 9], [10, 82]) → [3, 9, 10, 82] └─ merge([27, 38, 43], [3, 9, 10, 82]) → [3, 9, 10, 27, 38, 43, 82]

2. 병합 (Merge) 이제, 작은 배열부터 차례로 병합하며 정렬된 배열을 완성한다.

   1. [27] 과 [43] 병합 → [27, 43]
   2. [38] 과 [27, 43] 병합 → [27, 38, 43]
   3. [3] 과 [9] 병합 → [3, 9]
   4. [82] 과 [10] 병합 → [10, 82]
   5. [3, 9] 과 [10, 82] 병합 → [3, 9, 10, 82]
   6. [27, 38, 43] 과 [3, 9, 10, 82] 병합 → [3, 9, 10, 27, 38, 43, 82]

병합 정렬의 최적화 방법

1. 작은 배열에 대한 최적화
   작은 크기의 배열(일반적으로 크기가 10~20 이하)에 대해서는 삽입 정렬과 같은 더 간단한 정렬 알고리즘을 사용하여 성능을 개선할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def optimized_merge_sort(arr):
    # 작은 배열에 대해 삽입 정렬 사용
    if len(arr) <= 10:
        return insertion_sort(arr)
    
    # 이하 기존 병합 정렬과 동일
    mid = len(arr) // 2
    left_half = optimized_merge_sort(arr[:mid])
    right_half = optimized_merge_sort(arr[mid:])
    
    return merge(left_half, right_half)

1. 제자리 병합 정렬
   추가 메모리 사용을 줄이기 위해 제자리(in-place) 병합 정렬을 구현할 수도 있다. 하지만 이는 구현이 복잡하고 성능이 저하될 수 있다.

병합 정렬의 응용

1. 외부 정렬(External Sorting)
   병합 정렬은 대용량 데이터를 다룰 때 유용한 외부 정렬 알고리즘의 기초가 된다.
   주 메모리보다 큰 데이터를 처리할 때 사용된다.

2. 병렬 정렬
   병합 정렬은 병렬 처리에 적합한 구조를 가지고 있어, 다중 코어 환경에서 효율적으로 구현할 수 있다.

3. 역순 쌍 계산
   병합 정렬은 배열 내의 역순 쌍(inversion pairs)을 계산하는 데에도 활용될 수 있다.

참고 및 출처