삽입 정렬 (Insertion Sort)

삽입 정렬 (Insertion Sort)

삽입 정렬은 간단하면서도 직관적인 정렬 알고리즘으로, 실생활에서 카드 게임을 할 때 손에 든 카드를 정렬하는 방식과 매우 유사하다.

삽입 정렬은 간단하고 직관적인 정렬 알고리즘으로, 작은 데이터셋이나 거의 정렬된 데이터에서 효율적으로 작동한다.
비록 큰 데이터셋에서는 O(n²)의 시간 복잡도로 인해 퀵 정렬, 합병 정렬, 힙 정렬 등에 비해 느리지만, 그 단순함과 특정 상황에서의 효율성으로 인해 여전히 중요한 알고리즘이다.

실제 응용에서는 종종 다른 정렬 알고리즘과 함께 하이브리드 접근 방식으로 사용되며, 이를 통해 더 나은 성능을 얻을 수 있다. 또한 이진 탐색을 활용한 최적화나 셸 정렬과 같은 변형을 통해 성능을 향상시킬 수 있다.

정렬 알고리즘을 선택할 때는 데이터의 크기, 초기 정렬 상태, 메모리 제약 등 여러 요소를 고려해야 하며, 삽입 정렬은 이러한 고려 사항에 따라 여전히 유용한 선택지가 될 수 있다.

삽입 정렬의 기본 개념

삽입 정렬은 배열을 정렬된 부분과 정렬되지 않은 부분으로 나누고, 정렬되지 않은 부분의 요소를 하나씩 정렬된 부분의 적절한 위치에 삽입하는 방식으로 동작한다.

실생활에서의 예시로 설명하자면, 여러분이 손에 든 카드를 정렬할 때 사용하는 방법과 매우 유사하다. 카드를 하나씩 뽑아 이미 정렬된 카드들 사이의 올바른 위치에 삽입하는 것처럼, 삽입 정렬도 같은 원리로 작동한다.

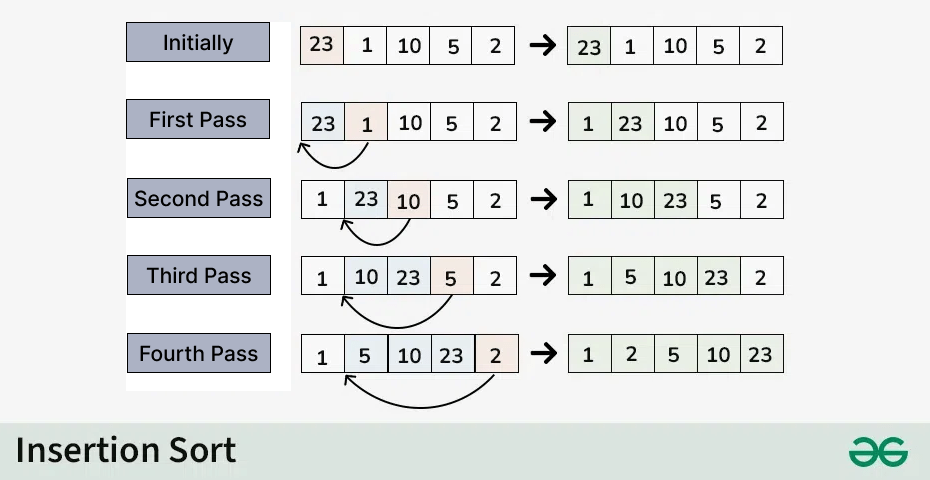
삽입 정렬의 알고리즘

삽입 정렬의 기본 알고리즘은 다음과 같다:

1. 두 번째 요소부터 시작한다. (첫 번째 요소는 이미 “정렬된” 것으로 간주)
2. 현재 요소를 정렬된 부분의 요소들과 비교하여 적절한 위치를 찾는다.
3. 적절한 위치를 찾으면, 그 위치에 현재 요소를 삽입하기 위해 필요한 만큼 요소들을 오른쪽으로 이동시킨다.
4. 현재 요소를 찾은 위치에 삽입한다.
5. 모든 요소에 대해 2~4 단계를 반복한다.

삽입 정렬의 동작 과정

배열을 삽입 정렬로 정렬하는 과정을 단계별로 살펴보면:

초기 배열:

1

[5, 2, 4, 6, 1, 3]

1. 첫 번째 요소(5)는 이미 정렬된 상태로 간주

   1	[5, 2, 4, 6, 1, 3] (5은 혼자 있어서 정렬 완료)

2. 두 번째 요소(2)를 적절한 위치에 삽입

   • 2와 5를 비교: 2 < 5
   • 5를 오른쪽으로 이동: [5, 5, 4, 6, 1, 3]
   • 2를 올바른 위치에 삽입: [2, 5, 4, 6, 1, 3]

   1	[2, 5, 4, 6, 1, 3]

3. 세 번째 요소(4)는 이미 정렬된 위치에 있음

   • 4와 5를 비교: 4 < 5
   • 5를 오른쪽으로 이동: [2, 5, 5, 6, 1, 3]
   • 4와 2를 비교: 4 > 2
   • 4를 올바른 위치에 삽입: [2, 4, 5, 6, 1, 3]

   1	[2, 4, 5, 6, 1, 3]

4. 네 번째 요소(6)를 적절한 위치에 삽입

   • 6과 5를 비교: 6 > 5
   • 6은 이미 올바른 위치에 있음: [2, 4, 5, 6, 1, 3]

   1	[2, 4, 5, 6, 1, 3]

5. 다섯 번째 요소(1)를 적절한 위치에 삽입

   • 1과 6, 5, 4, 2를 각각 비교: 1 < 2
   • 6, 5, 4, 2를 오른쪽으로 이동: [2, 4, 5, 6, 6, 3] -> [2, 4, 5, 5, 6, 3] -> [2, 4, 4, 5, 6, 3] -> [2, 2, 4, 5, 6, 3]
   • 1을 올바른 위치에 삽입: [1, 2, 4, 5, 6, 3]

   1	[1, 2, 4, 5, 6, 3]

6. 여섯 번째 요소(3)를 적절한 위치에 삽입

   • 3과 6, 5, 4를 각각 비교: 3 < 4
   • 6, 5, 4를 오른쪽으로 이동: [1, 2, 4, 5, 6, 6] -> [1, 2, 4, 5, 5, 6] -> [1, 2, 4, 4, 5, 6]
   • 3과 2를 비교: 3 > 2
   • 3을 올바른 위치에 삽입: [1, 2, 3, 4, 5, 6]

   1	[1, 2, 3, 4, 5, 6]

최종 정렬된 배열

1

[1, 2, 3, 4, 5, 6]

삽입 정렬의 구현

파이썬으로 구현한 삽입 정렬

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def insertion_sort(arr):
    # 첫 번째 요소는 이미 정렬된 것으로 간주하므로 두 번째 요소부터 시작
    for i in range(1, len(arr)):
        # 현재 요소를 key로 저장
        key = arr[i]
        
        # 정렬된 부분에서 key보다 큰 요소들을 찾아 오른쪽으로 이동
        j = i - 1
        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1
        
        # key를 찾은 위치에 삽입
        arr[j + 1] = key
    
    return arr

자바스크립트로 구현한 삽입 정렬

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

function insertionSort(arr) {
    const n = arr.length;
    
    for (let i = 1; i < n; i++) {
        // 현재 요소를 key로 저장
        const key = arr[i];
        
        // 정렬된 부분에서 key보다 큰 요소들을 찾아 오른쪽으로 이동
        let j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        
        // key를 찾은 위치에 삽입
        arr[j + 1] = key;
    }
    
    return arr;
}

삽입 정렬의 성능 분석

1. 시간 복잡도

   • 최선의 경우(이미 정렬된 배열): O(n)
     • 각 요소는 자신의 왼쪽에 있는 요소와 한 번씩만 비교하면 됨
   • 평균의 경우: O(n²)
     • 평균적으로 각 요소는 자신의 왼쪽에 있는 요소들의 절반 정도와 비교됨
   • 최악의 경우(역순으로 정렬된 배열): O(n²)
     • 각 요소는 자신의 왼쪽에 있는 모든 요소와 비교됨

2. 공간 복잡도
   삽입 정렬은 제자리(in-place) 정렬 알고리즘으로, 추가적인 메모리 공간을 거의 사용하지 않는다. 따라서 공간 복잡도는 O(1)이다.

3. 안정성
   삽입 정렬은 안정적(stable)인 정렬 알고리즘이다. 즉, 동일한 값을 가진 요소들의 상대적 순서가 정렬 과정에서 유지된다. 이는 동일한 값을 가진 요소를 만났을 때 그 요소를 넘어가지 않고 그대로 두기 때문이다.

삽입 정렬의 장단점

장점

1. 단순한 구현: 삽입 정렬은 이해하기 쉽고 구현이 간단하다.
2. 적은 메모리 사용: 추가적인 메모리 공간을 거의 사용하지 않는다.
3. 안정적인 정렬: 동일한 값을 가진 요소들의 상대적 순서가 유지된다.
4. 온라인 알고리즘: 데이터가 하나씩 들어올 때 정렬된 상태를 유지하면서 새 데이터를 적절한 위치에 삽입할 수 있다.
5. 작은 데이터셋에 효율적: 작은 배열에서는 퀵 정렬이나 합병 정렬과 같은 복잡한 알고리즘보다 더 효율적일 수 있다.
6. 거의 정렬된 배열에 매우 효율적: 이미 부분적으로 정렬된 배열에서는 O(n)에 가까운 성능을 보인다.

단점

1. 큰 데이터셋에 비효율적: 큰 배열에서는 O(n²)의 시간 복잡도로 인해 퀵 정렬, 합병 정렬, 힙 정렬 등에 비해 느리다.
2. 비교 횟수가 많음: 각 요소를 삽입할 때마다 이미 정렬된 부분의 요소들과 많은 비교를 수행해야 한다.
3. 원소 이동이 많음: 새로운 요소를 삽입할 위치를 찾은 후, 그 위치 이후의 모든 요소를 한 칸씩 옮겨야 한다.

실제 구현에서의 고려사항

1. 캐시 지역성(Cache Locality)
   삽입 정렬은 연속된 메모리 위치에 접근하는 특성으로 인해 캐시 지역성이 좋다.
   이는 현대 컴퓨터 아키텍처에서 성능에 유리하게 작용할 수 있다.

2. 재귀 vs. 반복
   삽입 정렬은 일반적으로 반복적(iterative) 방식으로 구현되지만, 재귀적(recursive) 구현도 가능하다.
   재귀적 구현은 다음과 같다:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

   def recursive_insertion_sort(arr, n=None): if n is None: n = len(arr) # 기저 조건: 배열의 크기가 1이면 이미 정렬됨 if n <= 1: return # 크기가 n-1인 배열을 재귀적으로 정렬 recursive_insertion_sort(arr, n - 1) # 마지막 요소를 정렬된 배열의 적절한 위치에 삽입 key = arr[n - 1] j = n - 2 while j >= 0 and arr[j] > key: arr[j + 1] = arr[j] j -= 1 arr[j + 1] = key return arr

3. 병렬화 가능성
   삽입 정렬은 본질적으로 순차적인 알고리즘으로, 병렬화하기 어렵다. 하지만 셸 정렬과 같은 변형을 통해 부분적인 병렬화가 가능할 수 있다.

삽입 정렬의 최적화 기법

1. 이진 탐색을 활용한 최적화
   삽입 정렬에서 새로운 요소의 위치를 찾기 위해 선형 탐색 대신 이진 탐색(Binary Search)을 사용할 수 있다.
   이를 통해 비교 횟수를 O(n²)에서 O(n log n)으로 줄일 수 있지만, 요소 이동(shift) 연산은 여전히 O(n²)이다.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

   def binary_insertion_sort(arr): for i in range(1, len(arr)): key = arr[i] # 이진 탐색으로 key가 들어갈 위치 찾기 left, right = 0, i - 1 while left <= right: mid = (left + right) // 2 if arr[mid] > key: right = mid - 1 else: left = mid + 1 # key가 들어갈 위치는 left # left부터 i-1까지의 요소들을 오른쪽으로 이동 for j in range(i - 1, left - 1, -1): arr[j + 1] = arr[j] arr[left] = key return arr

2. 셸 정렬(Shell Sort)
   셸 정렬은 삽입 정렬의 개선된 버전으로, 큰 간격으로 요소들을 부분 정렬한 후 점점 간격을 줄여가며 정렬한다. 이를 통해 요소의 이동 거리를 줄이고 성능을 향상시킬 수 있다.

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

   def shell_sort(arr): n = len(arr) gap = n // 2 while gap > 0: for i in range(gap, n): temp = arr[i] j = i while j >= gap and arr[j - gap] > temp: arr[j] = arr[j - gap] j -= gap arr[j] = temp gap //= 2 return arr

삽입 정렬의 응용 분야

1. 작은 데이터셋 정렬
   삽입 정렬은 작은 배열이나 리스트를 정렬할 때 효율적이다.
   실제로 많은 고급 정렬 알고리즘(퀵 정렬, 합병 정렬 등)은 작은 부분 배열을 처리할 때 삽입 정렬로 전환하는 최적화 기법을 사용한다.

2. 거의 정렬된 데이터 처리
   삽입 정렬은 이미 부분적으로 정렬된 데이터에서 매우 효율적이다. 온라인 트랜잭션 처리, 스트리밍 데이터 등 실시간으로 들어오는 데이터를 정렬된 상태로 유지해야 하는 경우에 유용하다.

3. 하이브리드 정렬 알고리즘
   많은 고성능 정렬 구현에서는 큰 데이터셋에는 퀵 정렬이나 합병 정렬을 사용하고, 작은 부분 배열에는 삽입 정렬을 사용하는 하이브리드 접근 방식을 채택한다. 자바의 Arrays.sort()와 같은 표준 라이브러리 함수도 이러한 방식을 사용한다.

4. 일상적인 정렬 작업
   카드 게임에서 손에 든 카드를 정렬하는 방식이나, 작은 목록을 수작업으로 정렬할 때 사람들이 자연스럽게 사용하는 방식과 유사하여, 직관적이고 이해하기 쉬운 알고리즘이다.

참고 및 출처