버블 정렬 (Bubble Sort)

버블 정렬은 가장 간단하고 직관적인 정렬 알고리즘 중 하나이다.
이름에서 알 수 있듯이, 마치 물속에서 공기 방울이 떠오르는 것처럼 큰 값들이 배열의 끝으로 ‘부글부글’ 올라가는 모습을 연상시킨다.
이 알고리즘은 단순함 때문에 컴퓨터 과학 입문 과정에서 가장 먼저 배우는 정렬 알고리즘이지만, 실제 응용에서는 비효율성 때문에 잘 사용되지 않는다. 그럼에도 불구하고, 버블 정렬의 작동 방식과 특성을 이해하는 것은 다른 정렬 알고리즘의 기초를 다지는 데 중요하다.

버블 정렬은 가장 단순한 정렬 알고리즘 중 하나로, 구현이 쉽고 이해하기 직관적이다. 그러나 O(n²)의 시간 복잡도로 인해 대규모 데이터셋에서는 비효율적이며, 실제 응용에서는 퀵 정렬, 병합 정렬, 힙 정렬과 같은 더 효율적인 알고리즘들이 선호된다.

그럼에도 불구하고, 버블 정렬은 정렬 알고리즘의 기본 개념을 이해하는 데 중요한 역할을 하며, 최적화 버전은 특정 상황(예: 거의 정렬된 작은 데이터셋)에서 실용적일 수 있다. 또한, 버블 정렬의 작동 방식을 이해하면 더 복잡한 정렬 알고리즘의 기초를 다지는 데 도움이 된다.

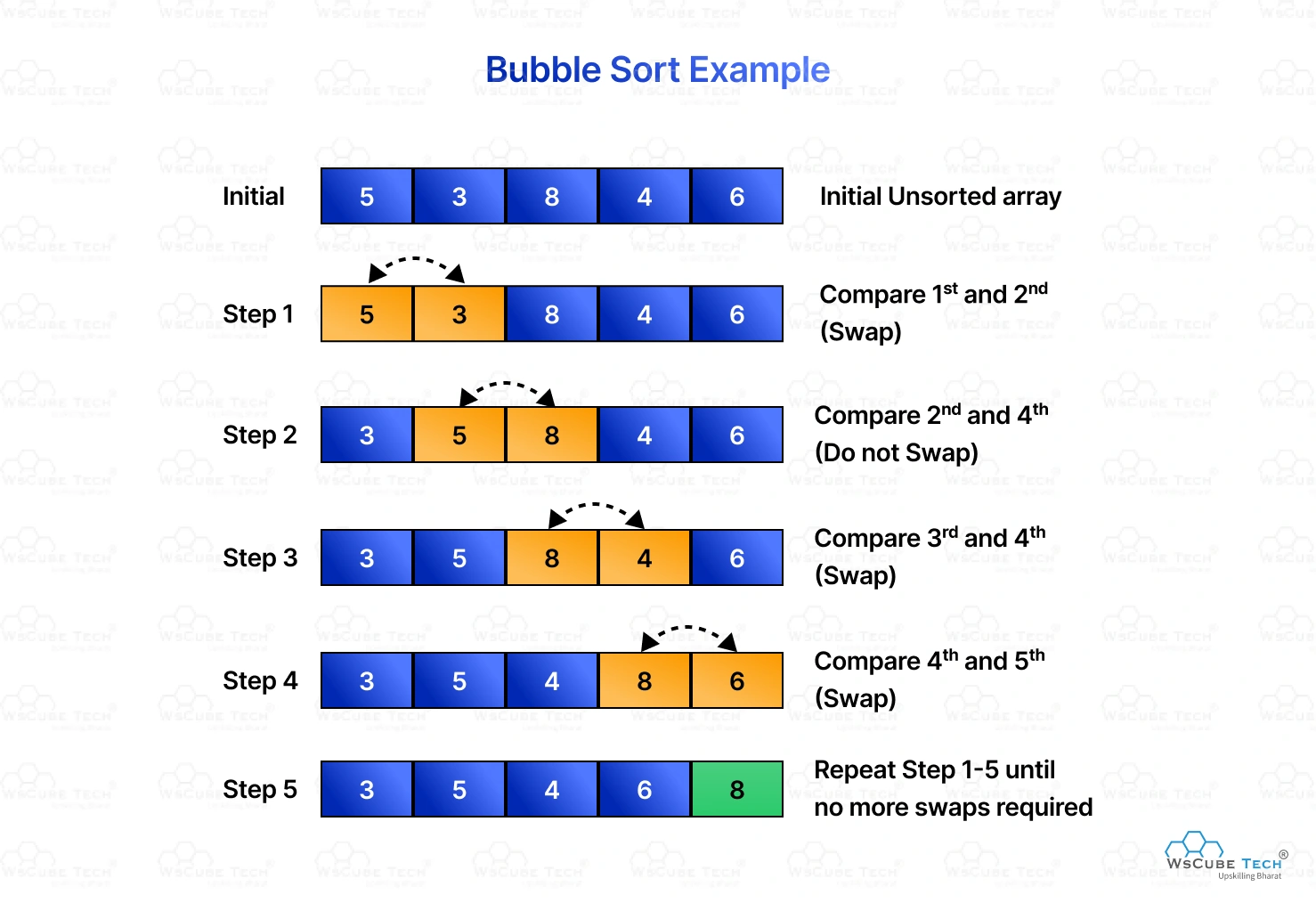
Bubble Sort — https://www.wscubetech.com/resources/dsa/bubble-sort

버블 정렬의 기본 원리

버블 정렬은 인접한 두 요소를 반복적으로 비교하고, 필요한 경우 위치를 교환하는 과정을 통해 정렬을 수행한다.
이 과정에서 가장 큰 요소가 마치 거품처럼 배열의 끝으로 ‘떠오르게’ 된다.

알고리즘 단계

배열의 첫 번째 요소부터 시작하여 인접한 요소와 비교한다.
현재 요소가 다음 요소보다 크면, 두 요소의 위치를 교환한다.
다음 쌍의 요소로 이동하여 1-2 과정을 반복한다.
배열의 끝에 도달하면, 가장 큰 요소가 배열의 마지막 위치에 정렬된다.
위 과정을 배열의 크기-1만큼 반복한다.

기본 구현(Python)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def bubble_sort(arr):
    n = len(arr)
    
    # 배열의 모든 요소를 순회
    for i in range(n):        
        # 이미 정렬된 요소는 다시 비교하지 않기 위해 n-i-1까지만 반복
        for j in range(0, n-i-1):            
            # 인접한 요소 비교 및 교환
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    
    return arr

버블 정렬의 작동 방식 예시

예를 들어, [5, 3, 8, 4, 2]라는 배열을 정렬해보자.

1차 패스:

[5, 3, 8, 4, 2] → 5 > 3이므로 교환 → [3, 5, 8, 4, 2]
[3, 5, 8, 4, 2] → 5 < 8이므로 유지 → [3, 5, 8, 4, 2]
[3, 5, 8, 4, 2] → 8 > 4이므로 교환 → [3, 5, 4, 8, 2]
[3, 5, 4, 8, 2] → 8 > 2이므로 교환 → [3, 5, 4, 2, 8]
1차 패스 후 가장 큰 값인 8이 배열의 끝에 위치하게 된다.

2차 패스:

[3, 5, 4, 2, 8] → 3 < 5이므로 유지 → [3, 5, 4, 2, 8]
[3, 5, 4, 2, 8] → 5 > 4이므로 교환 → [3, 4, 5, 2, 8]
[3, 4, 5, 2, 8] → 5 > 2이므로 교환 → [3, 4, 2, 5, 8]
2차 패스 후 두 번째로 큰 값인 5가 정렬된다.

3차 패스:

[3, 4, 2, 5, 8] → 3 < 4이므로 유지 → [3, 4, 2, 5, 8]
[3, 4, 2, 5, 8] → 4 > 2이므로 교환 → [3, 2, 4, 5, 8]

4차 패스:

[3, 2, 4, 5, 8] → 3 > 2이므로 교환 → [2, 3, 4, 5, 8]

최종적으로 배열은 [2, 3, 4, 5, 8]로 정렬된다.

버블 정렬의 시각화 및 이해

버블 정렬의 작동 방식을 시각적으로 이해하면 더 명확해진다.
각 패스마다 큰 값이 마치 거품처럼 위로 떠올라 배열의 끝으로 이동하는 모습을 상상해보면 된다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
초기 배열: [5, 3, 8, 4, 2]

1차 패스:
[3, 5, 8, 4, 2] (5와 3 교환)
[3, 5, 8, 4, 2] (5와 8 유지)
[3, 5, 4, 8, 2] (8과 4 교환)
[3, 5, 4, 2, 8] (8과 2 교환) -> 8이 올바른 위치에 정렬됨

2차 패스:
[3, 5, 4, 2, 8] (3과 5 유지)
[3, 4, 5, 2, 8] (5와 4 교환)
[3, 4, 2, 5, 8] (5와 2 교환) -> 5가 올바른 위치에 정렬됨

3차 패스:
[3, 4, 2, 5, 8] (3과 4 유지)
[3, 2, 4, 5, 8] (4와 2 교환) -> 4가 올바른 위치에 정렬됨

4차 패스:
[2, 3, 4, 5, 8] (3과 2 교환) -> 3이 올바른 위치에 정렬됨

최종 정렬된 배열: [2, 3, 4, 5, 8]

버블 정렬의 최적화

조기 종료(Early Termination)

기본 버블 정렬 알고리즘은 이미 배열이 정렬되었더라도 모든 패스를 실행한다.
그러나 한 번의 패스에서 교환이 일어나지 않았다면, 이는 배열이 이미 정렬되었다는 의미이다.
이 특성을 활용하여 알고리즘을 최적화할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
def optimized_bubble_sort(arr):
    n = len(arr)
    
    for i in range(n):
        # 교환이 발생했는지 추적하는 플래그
        swapped = False
        
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
                swapped = True
        
        # 교환이 없었다면 이미 정렬된 상태이므로 종료
        if not swapped:
            break
    
    return arr

칵테일 셰이커 정렬(Cocktail Shaker Sort)

버블 정렬의 또 다른 변형인 칵테일 셰이커 정렬은 양방향으로 작동한다.
한 번은 가장 큰 요소를 뒤로 이동시키고, 다음에는 가장 작은 요소를 앞으로 이동시키는 방식이다.
이는 ‘거북이 현상’(정렬 과정에서 작은 값이 배열의 앞으로 이동하는 데 오래 걸리는 현상)을 완화할 수 있다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def cocktail_shaker_sort(arr):
    n = len(arr)
    swapped = True
    start = 0
    end = n - 1
    
    while swapped:
        # 왼쪽에서 오른쪽으로 이동 (버블 업)
        swapped = False
        for i in range(start, end):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                swapped = True
        
        if not swapped:
            break
        
        end -= 1
        swapped = False
        
        # 오른쪽에서 왼쪽으로 이동 (버블 다운)
        for i in range(end - 1, start - 1, -1):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                swapped = True
        
        start += 1
    
    return arr

버블 정렬의 성능 분석

시간 복잡도

최선의 경우(이미 정렬된 배열): O(n)
- 최적화된 버전에서는 첫 번째 패스에서 교환이 없음을 감지하고 종료한다.
평균 및 최악의 경우: O(n²)
- 역순으로 정렬된 배열에서는 모든 비교와 교환이 필요하다.

공간 복잡도

O(1): 추가적인 메모리 공간을 거의 사용하지 않는 제자리(in-place) 정렬 알고리즘이다.

안정성

버블 정렬은 안정적인(stable) 정렬 알고리이다.
즉, 동일한 값을 가진 요소들의 상대적인 순서가 정렬 후에도 유지된다.
이는 버블 정렬이 인접한 요소끼리만 교환하기 때문이다.

버블 정렬의 장단점

장점

간단한 구현: 코드가 직관적이고 이해하기 쉽다.
제자리 정렬: 추가 메모리가 거의 필요하지 않는다.
안정적인 정렬: 동일한 값의 상대적 순서가 유지된다.
적응성: 이미 부분적으로 정렬된 배열에 대해 최적화된 버전이 효율적으로 작동할 수 있다.

단점

비효율성: O(n²)의 시간 복잡도로 대규모 데이터셋에서 매우 느리다.
많은 교환 연산: 다른 정렬 알고리즘에 비해 데이터 교환이 많아 비효율적이다.
실용성 부족: 실제 응용에서는 거의 사용되지 않으며, 주로 교육 목적으로만 사용된다.

버블 정렬의 응용 및 실제 사용 사례

버블 정렬은 주로 다음과 같은 상황에서 고려될 수 있다:

교육 목적: 정렬 알고리즘의 기초 개념을 가르치는 데 이상적이다.
소규모 데이터셋: 요소가 매우 적은 배열(보통 10개 미만)에서는 구현의 단순함 때문에 사용될 수 있다.
거의 정렬된 데이터: 최적화된 버블 정렬은 이미 대부분 정렬된 데이터에서 효율적일 수 있다.
제한된 환경: 메모리가 매우 제한된 환경에서는 구현이 단순한 버블 정렬이 선택될 수 있다.

버블 정렬의 다양한 구현

JavaScript 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
function bubbleSort(arr) {
    const n = arr.length;
    
    for (let i = 0; i < n; i++) {
        // 최적화: 교환 발생 여부 추적
        let swapped = false;
        
        for (let j = 0; j < n - i - 1; j++) {
            // 인접 요소 비교 및 교환
            if (arr[j] > arr[j + 1]) {
                // 교환 (ES6 구문 활용)
                [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
                swapped = true;
            }
        }
        
        // 교환이 없었다면 이미 정렬된 상태
        if (!swapped) break;
    }
    
    return arr;
}

Java 구현

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
public static int[] bubbleSort(int[] arr) {
    int n = arr.length;
    
    for (int i = 0; i < n; i++) {
        boolean swapped = false;
        
        for (int j = 0; j < n - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                // 교환
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                swapped = true;
            }
        }
        
        // 교환이 없었다면 종료
        if (!swapped) break;
    }
    
    return arr;
}