복잡도 클래스(Complexity Classes)
복잡도 클래스(Complexity Classes)는 계산 이론의 핵심 개념으로, 문제 해결에 필요한 계산 자원(시간, 공간 등)의 양에 따라 문제들을 분류하는 체계이다.
복잡도 클래스는 계산 복잡도 이론의 핵심 개념으로, 알고리즘과 문제의 복잡성을 분류하고 이해하는 데 중요한 역할을 한다. 이 분야는 컴퓨터 과학에서 “무엇이 효율적으로 계산 가능한가?“라는 근본적인 질문을 다룬다.
알고리즘의 효율성 분석과 문제 간의 관계 이해에 기여하며, 특히 P vs NP 문제와 같은 근본적인 질문을 탐구하는 기반이 된다. P vs NP 문제를 비롯한 미해결 과제들은 인공지능, 암호학, 최적화 분야에 직간접적 영향을 미친다.
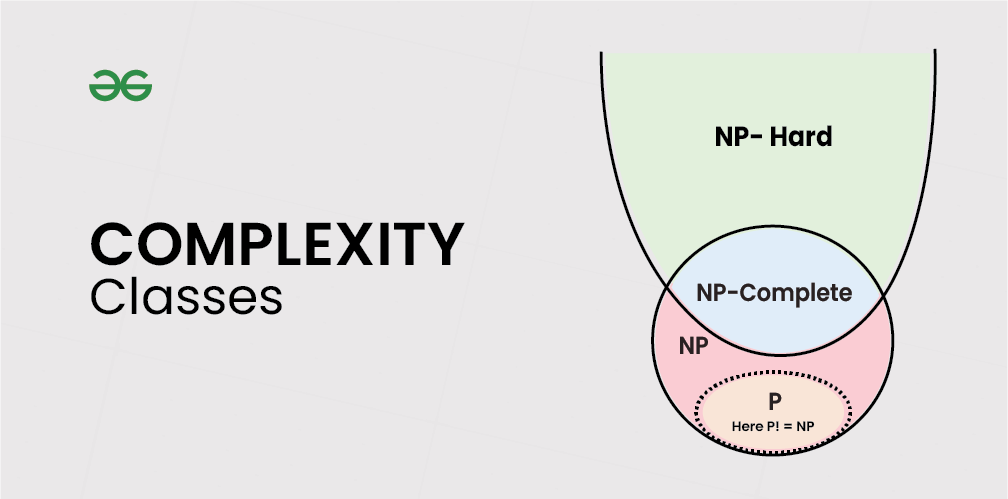
주요 복잡도 클래스
L ⊆ NL ⊆ P ⊆ NP ⊆ PSPACE = NPSPACE ⊆ EXPTIME ⊆ EXPSPACE
P (Polynomial Time)
- 정의: 결정론적 튜링 머신에서 다항 시간에 해결할 수 있는 문제들의 집합
- 특징: 효율적으로 해결 가능한 문제들
- 예시: 정렬(Sorting), 이진 검색(Binary Search), 최단 경로 찾기(Shortest Path)
- 수학적 표현: P = { L | L은 다항 시간 안에 결정론적 튜링 머신으로 결정 가능 }
NP (Non-deterministic Polynomial Time)
- 정의: 비결정론적 튜링 머신에서 다항 시간에 해결할 수 있는 문제들의 집합
- 특징: 해답이 주어지면 다항 시간 내에 검증 가능한 문제들
- 예시: 부분집합 합 문제(Subset Sum), 해밀턴 경로(Hamiltonian Path), 배낭 문제(Knapsack Problem)
- 수학적 표현: NP = { L | L은 다항 시간 안에 비결정론적 튜링 머신으로 결정 가능 }
NP-완전(NP-Complete)
- 정의: NP의 모든 문제가 다항 시간 내에 환원(reduce)될 수 있는 NP 문제들의 집합
- 특징: NP에서 가장 어려운 문제들로, 하나라도 다항 시간에 해결되면 모든 NP 문제가 다항 시간에 해결됨
- 예시: 3SAT(Boolean Satisfiability Problem), 순회 판매원 문제(Traveling Salesman Problem)
- 중요성: P=NP 문제의 핵심
NP-난해(NP-Hard)
- 정의: 적어도 NP 문제만큼 어려운 문제들의 집합 (NP에 속할 필요는 없음)
- 특징: NP의 모든 문제가 다항 시간 내에 이 문제로 환원될 수 있음
- 예시: 일반 형태의 순회 판매원 문제, 최적 스케줄링
PSPACE
- 정의: 다항 공간에 해결할 수 있는 문제들의 집합
- 특징: P ⊆ NP ⊆ PSPACE
- 예시: 양자화된 불리언 공식(TQBF), 일부 게임 전략
PSPACE는 NP를 포함하지만, 실제로 NP와의 관계는 명확하지 않다.
PSPACE-완전 문제(예: 양자 회로 시뮬레이션)는 이론적으로 지수 시간이 필요하지만, 다항 공간만 사용한다는 점에서 NP-완전 문제와 구별된다.
예를 들어, QBF(Quantified Boolean Formula) 문제는 PSPACE-완전으로, 모든 가능한 변수 할당을 재귀적으로 검토하지만 공간 재사용을 통해 메모리 사용을 최적화한다.
EXPTIME
- 정의: 지수 시간에 해결할 수 있는 문제들의 집합
- 특징: PSPACE ⊆ EXPTIME
- 예시: 체스와 같은 복잡한 게임에서 최적의 움직임 찾기
복잡도 클래스 간의 관계
현재까지 알려진 복잡도 클래스 간의 관계는 다음과 같다:
L ⊆ NL ⊆ P ⊆ NP ⊆ PSPACE ⊆ EXPTIME ⊆ NEXPTIME ⊆ EXPSPACE
- L(Logarithmic Space): 로그 공간으로 해결 가능한 문제들 (예: 그래프 연결성 검사).
- PSPACE: 다항 공간으로 해결 가능한 문제들 (예: 양자 게임 이론의 특정 문제).
- EXPTIME: 지수 시간이 필요한 문제들 (예: 체스의 완전한 전략 수립).
그러나 이 포함 관계 중 어느 것이 진정한 부분집합(⊂)인지는 아직 증명되지 않았다.
이 중 가장 유명한 미해결 문제가 P=NP 문제이다.
P=NP 문제
컴퓨터 과학에서 가장 중요한 미해결 문제 중 하나:
- 문제: P와 NP가 동일한 클래스인가?
- 의미: 만약 P=NP라면, 우리가 효율적으로 검증할 수 있는 모든 문제를 효율적으로 해결할 수도 있다는 의미
- 영향: 만약 P=NP가 증명된다면, 암호학, 최적화, 인공지능 등 많은 분야에 혁명적인 변화가 일어날 것
- 현재 상태: 대부분의 컴퓨터 과학자들은 P≠NP라고 믿지만, 아직 증명되지 않았다.
랜덤화 복잡도 클래스
알고리즘이 랜덤성을 활용할 수 있을 때 등장하는 클래스:
BPP (Bounded-error Probabilistic Polynomial Time)
- 다항 시간 내에 일정 확률로 올바른 답을 주는 문제들
P ⊆ BPP이며,BPP ⊆ PSPACE
RP (Randomized Polynomial Time)
- 다항 시간 내에 확률적으로 실행되지만, 긍정적인 답만 정확히 인식하는 문제들
P ⊆ RP ⊆ NP
ZPP (Zero-error Probabilistic Polynomial Time)
- 항상 올바른 답을 주며, 예상 실행 시간이 다항식인 문제들
ZPP = RP ∩ co-RP
병렬 계산 복잡도 클래스
여러 프로세서가 동시에 작업할 때의 복잡도 클래스:
- NC (Nick’s Class)
- 병렬 프로세서에서 다항 수의 프로세서와 다항 로그 시간 내에 해결 가능한 문제들
- 병렬화가 잘 되는 문제들의 클래스
- P-완전 문제들은 병렬화하기 어려운 문제들
양자 복잡도 클래스
양자 컴퓨터에서의 복잡도 클래스:
- BQP (Bounded-error Quantum Polynomial Time)
- 양자 컴퓨터에서 다항 시간 내에 일정 확률로 올바른 답을 주는 문제들
BPP ⊆ BQP ⊆ PSPACE- 소인수분해와 이산 로그 문제가 여기에 속함
복잡도 클래스의 실제 응용
복잡도 클래스 이론은 이론적인 것처럼 보이지만, 실제로 많은 응용이 있다:
암호학
현대 암호 시스템의 많은 부분이 P≠NP 가정에 기반한다. 만약 P=NP라면, RSA와 같은 많은 암호화 방식이 안전하지 않게 된다.최적화
많은 최적화 문제들이 NP-난해하기 때문에, 근사 알고리즘이나 휴리스틱 방법을 사용해야 한다.알고리즘 설계
문제의 복잡도 클래스를 이해하면 적절한 접근 방식을 선택하는 데 도움이 된다:- P 클래스 문제: 정확한 알고리즘을 찾는 데 집중
- NP-완전/NP-난해 문제: 근사 알고리즘, 휴리스틱, 매개변수화된 알고리즘 등을 고려
최근 연구 동향
복잡도 이론 분야의 최근 연구 동향은 다음과 같다:
세밀한 복잡도 이론(Fine-grained Complexity Theory)
P 클래스 내에서의 더 세밀한 구분을 연구한다.
예를 들어, 어떤 문제들이 정확히 O(n²) 시간이 필요하고, O(n²-ε)에는 해결할 수 없는지 연구한다.매개변수화된 복잡도(Parameterized Complexity)
문제의 복잡도를 입력 크기뿐만 아니라 다른 매개변수에 따라 분석한다.
이를 통해 NP-난해 문제라도 특정 매개변수가 고정될 때 효율적으로 해결할 수 있다.양자 우위(Quantum Supremacy)
양자 컴퓨터가 기존 컴퓨터보다 확실히 빠르게 해결할 수 있는 문제를 찾는 연구가 활발히 진행 중이다.